题目内容
【题目】已知平面直角坐标系中两个定点
，
，如果对于常数
，在函数
，
的图像上有且只有6个不同的点
，使得
成立，那么的取值范围是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
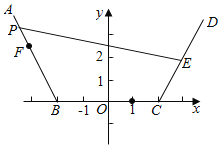
画出函数y＝|x+2|+|x﹣2|﹣4在[﹣4，4]的图象，讨论若P在AB上，设P（x，﹣2x﹣4）；若P在BC上，设P（x，0）；若P在CD上，设P（x，2x﹣4）．求得向量PE，PF的坐标，求得数量积，由二次函数的最值的求法，求得取值范围，讨论交点个数，即可得到所求范围．
函数y＝|x+2|+|x﹣2|﹣4
，
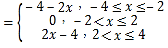（1）若P在AB上，设P（x，﹣2x﹣4），﹣4≤x≤﹣2．
∴
（3﹣x，6+2x），
（﹣3﹣x，6+2x）．
∴
x2﹣9+（6+2x）2＝5x2+24x+27=
，
∵x∈[﹣4，﹣2]，∴
λ≤11．
∴当λ
或
时有一解，当
λ≤-1时有两解；
（2）若P在BC上，设P（x，0），﹣2＜x≤2．
∴（3﹣x，2），（﹣3﹣x，2）．
∴x2﹣9+4＝x2﹣5，
∵﹣2＜x≤2，∴﹣5≤λ≤﹣1．
∴当λ＝﹣5或﹣1时有一解，当﹣5＜λ＜﹣1时有两解；
（3）若P在CD上，设P（x，2x﹣4），2＜x≤4．
（3﹣x，6﹣2x），（﹣3﹣x，6﹣2x），
∴x2﹣9+（6﹣2x）2＝5x2﹣24x+27，
∵2＜x≤4，∴λ≤11．
∴当λ或
时有一解，当λ<-1时有两解；
综上，可得有且只有6个不同的点P的情况是λ＜﹣1．
故选：C．
练习册系列答案
相关题目
