题目内容

偶函数f（x）的定义域为R，它在（0，+∞）是减函数，则下列不等式中成立的是（　　）
分析：由已知中偶函数f（x）的定义域为R，它在（0，+∞）是减函数，可得f(
3
4
)≥f(a2-a+1)，根据函数f（x）是偶函数，f(-
3
4
)=f(
3
4
)，可得答案．
解答：解：∵函数f（x）是偶函数
∴f(-
3
4
)=f(
3
4
)
又∵a2-a+1≥
3
4

∴f(
3
4
)≥f(a2-a+1)
∴f(-
3
4
)≥f(a2-a+1)
故选D
点评：本题考查的知识点是奇偶性与单调性的综合，其中判断出a2-a+1≥
3
4
是解答本题的关键．
练习册系列答案
相关题目
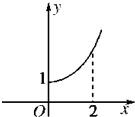精英家教网定义在R上的偶函数f（x）的部分图象如图所示，则在（-2，0）上，下列函数中与f（x）的单调性不同的是（　　）
A、y=x2+1
B、y=|x|+1
C、y=
2x+1，x≥0
x3+1，x＜0
D、y=
ex，x≥0
e-x，x＜0
设函数f（x）的定义在R上的偶函数，且是以4为周期的周期函数，当x∈[0，2]时，f（x）=2x-cosx，则a=f（-
3
2
）与b=f（
15
2
）的大小关系为
a＞b
a＞b
．
已知定义在R上的偶函数f（x）的最小值为1，当x∈[0，+∞）时，f（x）=aex．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）求最大的整数m（m＞1），使得存在t∈R，只要x∈[1，m]，就有f（x+t）≤ex．（注：e为自然对数的底数）
已知定义在R上的偶函数f （x）的单调减区间为[0，+∞），则不等式f（x）＜f（2-x）的解集是
（1，+∞）
（1，+∞）
．
已知定义在实数集R上的偶函数f（x）的最小值为3，且当x≥0时，f（x）=3ex+a（a为常数）．
（1）求函数f（x）的解析式；
（2）求最大的整数m（m＞1），使得存在实数t，对任意的x∈[1，m]都有f（x+t）＜3ex．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网