Question

已知函数f（x）=3sin（2x+

π

6

）-1，
（1）求函数f（x）的最小正周期；
（2）求函数f（x）的最大值及取得最大值时x的取值集合；
（3）求函数f（x）的单调递增区间；
（4）用五点法做出函数f（x）的图象，并说明该函数的图象可以由y=sinx的图象怎样变换得到？

Answer 1

分析：（1）直接利用周期公式求出函数的周期．
（2）利用正弦函数的最大值，求出函数的最大值，以及取得最大值时x的取值集合．
（3）利用正弦函数的单调增区间，求出函数的单调增区间．
（4）按照“五点法”作图方法做出函数f（x）的图象；按照y=sinx横坐标缩短

1

2

纵坐标不变，再向左平移，纵坐标伸长横坐标不变，图象向下平移即可．

解答：解：（1）T=

2π

2

=π
（2）当sin(2x+

π

6

)=1
即2x+

π

6

=

π

2

+2kπ，k∈Z
∴x=

π

6

+kπ，k∈Z，
∴y_max=2时，满足条件的x的集合为{x|x=

π

6

+kπ，k∈Z}
（3）因为2x+

π

6

∈[2kπ-

π

2

，2kπ+

π

2

]k∈Z，所以x∈[-

π

3

+kπ，

π

6

+kπ](k∈Z)，
所以单调递增区间为[-

π

3

+kπ，

π

6

+kπ](k∈Z)
（4）列表
函数图象为：

2x+ π 6	0	π 2	π	3π 2	2π
x	- π 12	π 6	5π 12	2π 3	11π 12
y	-1	1	-1	-3	-1

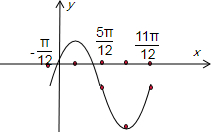
y=sinx，所有点的横坐标变为原来的

1

2

倍（纵坐标不变）
y=sin2x，所有点向左平移

π

12

个单位长度
y=sin(2x+

π

2

)，所有点的纵坐标变为原来的2倍（横坐标不变）
y=2sin(2x+

π

6

)，所有点向下平移1个单位
y=2sin(2x+

π

6

)-1

点评：本题是三角函数的综合题目，考查三角函数的周期、最值、单调增区间、函数的图象，图象的变换，考查学生的综合素质，计算解题能力．