题目内容
已知f(x)=2x可以表示成一个奇函数g(x)与一个偶函数h(x)之和,若关于x的不等式ag(x)+h(2x)≥0对于x∈[1,2]恒成立,则实数a的最小值是 .
【答案】分析:由题意可得g(x)+h(x)=2x①,g(-x)+h(-x)=-g(x)+h(x)=2-x②从而可得h(x)=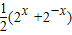 ,g(x)=
,g(x)=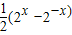
而ag(x)+h(2x)≥0对于x∈[1,2]恒成立即a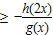 对于x∈[1,2]恒成立即
对于x∈[1,2]恒成立即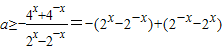 对于x∈[1,2]恒成立,只要求出函数
对于x∈[1,2]恒成立,只要求出函数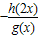 的最大值即可
的最大值即可
解答:解:f(x)=2x可以表示成一个奇函数g(x)与一个偶函数h(x)之和
∴g(x)+h(x)=2x①,g(-x)+h(-x)=-g(x)+h(x)=2-x②
①②联立可得,h(x)= ,g(x)=
,g(x)=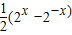
ag(x)+h(2x)≥0对于x∈[1,2]恒成立
a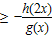 对于x∈[1,2]恒成立
对于x∈[1,2]恒成立
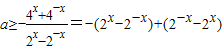 对于x∈[1,2]恒成立
对于x∈[1,2]恒成立
t=2x-2-x,x∈[1,2],t∈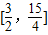 则t
则t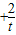 在t∈
在t∈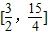 单调递增,
单调递增,
t= 时,则t
时,则t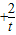 =
=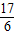
a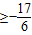
故答案为: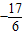
点评:本题主要考查了奇偶函数的定义的应用,函数的恒成立的问题,常会转化为求函数的最值问题,体现了转化思想的应用.
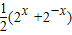 ,g(x)=
,g(x)=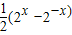
而ag(x)+h(2x)≥0对于x∈[1,2]恒成立即a
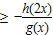 对于x∈[1,2]恒成立即
对于x∈[1,2]恒成立即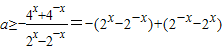 对于x∈[1,2]恒成立,只要求出函数
对于x∈[1,2]恒成立,只要求出函数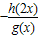 的最大值即可
的最大值即可解答:解:f(x)=2x可以表示成一个奇函数g(x)与一个偶函数h(x)之和
∴g(x)+h(x)=2x①,g(-x)+h(-x)=-g(x)+h(x)=2-x②
①②联立可得,h(x)=
 ,g(x)=
,g(x)=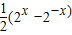
ag(x)+h(2x)≥0对于x∈[1,2]恒成立
a
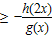 对于x∈[1,2]恒成立
对于x∈[1,2]恒成立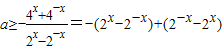 对于x∈[1,2]恒成立
对于x∈[1,2]恒成立t=2x-2-x,x∈[1,2],t∈
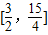 则t
则t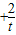 在t∈
在t∈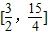 单调递增,
单调递增,t=
 时,则t
时,则t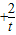 =
=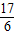
a
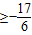
故答案为:
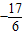
点评:本题主要考查了奇偶函数的定义的应用,函数的恒成立的问题,常会转化为求函数的最值问题,体现了转化思想的应用.

练习册系列答案
相关题目