题目内容
19.将函数y=sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位,再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),则所得函数图象对应的解析式为( )| A. | y=sin(x-$\frac{2π}{3}$) | B. | y=sin(x-$\frac{π}{3}$) | C. | y=sin4x | D. | y=sinx |
分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:将函数y=sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位,可得函数y=sin[2(x+$\frac{π}{6}$)-$\frac{π}{3}$]=sin2x的图象;
再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),则所得函数图象对应的解析式为y=sinx,
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
10.一个圆锥的体积是$\frac{π}{3}$,高是1,它的顶点和底面圆周在球O的球面上,则球O的表面积是( )
| A. | π | B. | 2π | C. | 4π | D. | 8π |
4.设$a={log_4}3,b={log_{0.4}}3,c={(\frac{1}{2})^2}$则a,b,c的大小关系是( )
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | a>c>b |
8.函数f(x)=tanωx(ω>0)的图象的相邻两支截直线y=2所得线段长为$\frac{π}{2}$,则f($\frac{π}{6}$)的值是( )
| A. | -$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
9.阅读如图的程序框图,运行相应的程序则输出的K和S值分别为( )
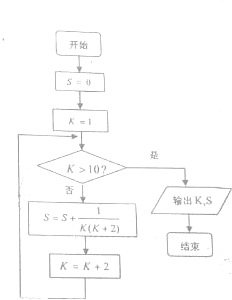

| A. | 9,$\frac{4}{9}$ | B. | 11,$\frac{5}{11}$ | C. | 13,$\frac{6}{13}$ | D. | 15,$\frac{7}{15}$ |