题目内容
4.设$a={log_4}3,b={log_{0.4}}3,c={(\frac{1}{2})^2}$则a,b,c的大小关系是( )| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | a>c>b |
分析 根据对数函数和指数函数的单调性,比较它们与0和1的大小关系,从而得到答案.
解答 解:∵0=log41<a=log43<log44=1,
b=log0•43<log0•41=0,
0<c=$(\frac{1}{2})^{2}=\frac{1}{4}=(lo{g}_{4}2)^{2}<lo{g}_{4}2<lo{g}_{4}3$,
∴a>c>b.
故选:D.
点评 本题考查了对数值和指数值大小的比较,考查了对数函数的单调性,是基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
15.执行如图所示的程序框图,若输入的x的值为3,则输出的n的值为( )
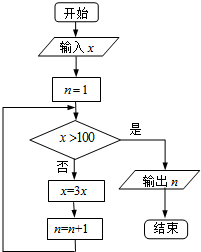

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
19.将函数y=sin(2x-$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位,再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),则所得函数图象对应的解析式为( )
| A. | y=sin(x-$\frac{2π}{3}$) | B. | y=sin(x-$\frac{π}{3}$) | C. | y=sin4x | D. | y=sinx |
9.若sinθ+cosθ=$\frac{\sqrt{5}}{5}$,θ∈[0,π],则tanθ=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
14.下列说法错误的是( )
| A. | 已知两个命题p,q,若p∧q为假命题,则p∨q也为假命题 | |
| B. | 实数a=0是直线ax-2y=1与2ax-2y=3平行的充要条件 | |
| C. | “?x0∈R,使得x02+2x0+5=0“的否定是“?x∈R,都有x2+2x+5≠0“ | |
| D. | 命题p:?x∈R,x2+1≥1;命题q:?x∈R,x2-x+1≤0,则命题p∧(¬q)是真命题 |