题目内容
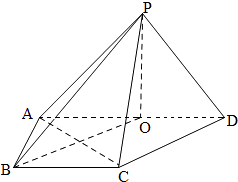
【题目】如图，在四棱锥P﹣ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD= 
，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，O为AD中点． 
（1）求证：PO⊥平面ABCD；
（2）求异面直线PB与CD所成角的余弦值；
（3）线段AD上是否存在点Q，使得它到平面PCD的距离为 
？若存在，求出 
的值；若不存在，请说明理由．
【答案】
（1）证明：在△PAD卡中PA=PD，O为AD中点，所以PO⊥AD．
又侧面PAD⊥底面ABCD，平面PAD∩平面ABCD=AD，PO平面PAD，
所以PO⊥平面ABCD．
（2）解：连接BO，在直角梯形ABCD中，BC∥AD，AD=2AB=2BC，
有OD∥BC且OD=BC，所以四边形OBCD是平行四边形，
所以OB∥DC．
由（1）知PO⊥OB，∠PBO为锐角，
所以∠PBO是异面直线PB与CD所成的角．
因为AD=2AB=2BC=2，在Rt△AOB中，AB=1，AO=1，所以OB= 
，
在Rt△POA中，因为AP= ，AO=1，所以OP=1，
在Rt△PBO中，PB= 
，所以cos∠PBO= 
，
所以异面直线PB与CD所成的角的余弦值为 ．
（3）解：假设存在点Q，使得它到平面PCD的距离为 
．
设QD=x，则S△DQC= 
x，由（2）得CD=OB= ，
在Rt△POC中，PC= ，
所以PC=CD=DP，S△PCD= 
= ，
由Vp﹣DQC=VQ﹣PCD，得x= 
，所以存在点Q满足题意，此时 
= 
．
【解析】（1）根据线面垂直的判定定理可知，只需证直线PO垂直平面ABCD中的两条相交直线垂直即可；（2）先通过平移将两条异面直线平移到同一个起点B，得到的锐角或直角就是异面直线所成的角，在三角形中再利用余弦定理求出此角即可；（3）利用Vp﹣DQC=VQ﹣PCD，即可得出结论．
【考点精析】本题主要考查了异面直线及其所成的角和直线与平面垂直的判定的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题．
