题目内容
【题目】已知函数f（x）=ax+ 
的图象经过点A（1，1），B（2，﹣1）．
（1）求函数f（x）的解析式；
（2）判断函数f（x）在（0，+∞）上的单调性并用定义证明；
（3）求f（x）在区间[ 
，1]上的值域．
【答案】
（1）解：∵f（x）的图象过A（1，1）、B（2，﹣1），
∴ 
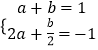，解得 
，
∴ 
（2）证明：设任意x1，x2∈（0，+∞），且x1＜x2，
f（x1）﹣f（x2）=（﹣x1+ 
）﹣（﹣x2+ 
）
=（x2﹣x1）+ 
= 
由x1，x2∈（0，+∞）得，x1x2＞0，x1x2+2＞0．
由x1＜x2得，x2﹣x1＞0，
∴f（x1）﹣f（x2）＞0，即f（x1）＞f（x2），
∴函数 在（0，+∞）上为减函数
（3）解：由（2）知，函数 在[ 
，1]上为减函数，
∴f（x）min=f（1）=1， 
，
∴f（x）的值域是 
【解析】（1）由待定系数法求出函数的解析式。（2）根据函数单调性的定义证明即可。（3）利用函数的单调性定义可得结果。
【考点精析】认真审题，首先需要了解奇偶性与单调性的综合(奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性)．
练习册系列答案
相关题目
