题目内容

设M={x|-2≤x≤2}，N={y|0≤y≤2}，函数f（x）的定义域为M，值域为N，则f（x）的图象可以是（ ）
A．
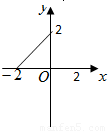
B．
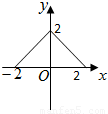
C．
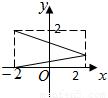
D．
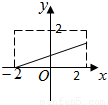
【答案】分析：可用排除法根据函数定义域、值域以及函数概念进行逐一验证可得答案．
解答：解：A项定义域为[-2，0]，D项值域不是[0，2]，C项对任一x都有两个y与之对应，都不符．
故选B．
点评：本题考查的是函数三要素，即定义域、值域、对应关系的问题．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
下列说法中：
①若定义在R上的函数f（x）满足f（x+2）=-f（x-1），则6为函数f（x）的周期；
②若对于任意x∈（1，3），不等式x2-ax+2＜0恒成立，则a＞
11
3
；
③定义：“若函数f（x）对于任意x∈R，都存在正常数M，使|f（x）|≤M|x|恒成立，则称函数f（x）为有界泛函．”由该定义可知，函数f（x）=x2+1为有界泛函；
④对于函数f(x)=
x-1
x+1
，设f2（x）=f[f（x）]，f3（x）=f[f2（x）]，…，fn+1（x）=f[fn（x）]（n∈N*且n≥2），令集合M={x|f2009（x）=x，x∈R}，则集合M为空集．
正确的个数为（　　）
A、1个B、2个C、3个D、4个
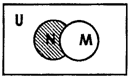精英家教网设全集U是实数集R，M={x|x＞2或x＜-2}，N={x|x2-4x+3＞0}则图中阴影部分所表示的集合是（　　）
A、{x|-2≤x＜1}B、{x|-2≤x≤2}C、{x|1＜x≤2}D、{x|x＜2}
下列说法中：
①若定义在R上的函数f（x）满足f（x+2）=-f（x-1），则6为函数f（x）的周期；
②若对于任意x∈（1，3），不等式x2-ax+2＜0恒成立，则a＞
11
3
；
③定义：“若函数f（x）对于任意x∈R，都存在正常数M，使|f（x）|≤M|x|恒成立，则称函数f（x）为有界泛函．”由该定义可知，函数f（x）=x2+1为有界泛函；
④对于函数f(x)=
x-1
x+1
，设f2（x）=f[f（x）]，f3（x）=f[f2（x）]，…，fn+1（x）=f[fn（x）]（n∈N*且n≥2），令集合M={x|f2009（x）=x，x∈R}，则集合M为空集．
正确的个数为（　　）
A．1个B．2个C．3个D．4个
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网