题目内容
一机器可以按各种不同的速度运转,其生产物件有一些会有缺点,每小时生产有缺点物件的多少随机器运转速度而变化,用
表示转速(单位转/秒),用
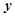表示每小时生产的有缺点物件个数,现观测得到
的4组观测值为(8,5),(12,8),(14,9),(16,11)．
(1)假定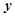与之间有线性相关关系,求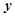对的回归直线方程．
(2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒?(精确到1转/秒)
(参考公式
)
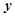表示转速(单位转/秒),用表示每小时生产的有缺点物件个数,现观测得到的4组观测值为(8,5),(12,8),(14,9),(16,11)．(1)假定
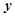与之间有线性相关关系,求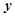对的回归直线方程．(2)若实际生产中所容许的每小时最大有缺点物件数为10,则机器的速度不得超过多少转/秒?(精确到1转/秒)
(参考公式
)（1）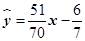
；（2）14转/秒
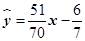；（2）14转/秒试题分析：（1）先求出横标和纵标的平均数，得到这组数据的样本中心点，利用最小二乘法求出线性回归方程的系数，代入样本中心点求出a的值，写出线性回归方程．
（2）由实际生产中所容许的每小时最大有缺陷物件数为l0，建立不等式进行求解即可．
(1)设回归直线方程为
,
,
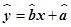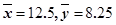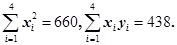于是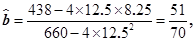
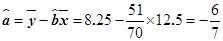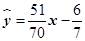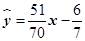所以所求的回归直线方程为．(2)由≤10,得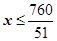
，即机器的速度不得超过14转/秒． 
练习册系列答案
轻松暑假总复习系列答案
相关题目
与
之间的一组抽样数据如下：
必过点( )
B．
C．
D．
＝－3.2x＋
，则
和判断力
进行统计分析，得下表数据：
中的
的值为
，则记忆力为
的同学的判断力约为（附：线性回归方程
，其中
、
为样本平均值)（ ）
B.
C.
（吨）与相应的生产能耗
(吨)的几组对应数据：
0.7
＝x＋1
，根据回归方程，预测加工70个零件所花费的时间为________分钟.