题目内容
定义在(0,+∞)上的单调递增函数f(x)满足:f(x)的导函数存在,且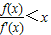 ,则下列不等式成立的是( )
,则下列不等式成立的是( )A.f(2)<2f(1)
B.3f(3)<4f(4)
C.2f(3)<3f(4)
D.3f(2)<2f(3)
【答案】分析:由f(x)是定义在(0,+∞)上的单调递增函数得到f′(x)>0在(0,+∞)上恒成立,则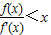 变形为xf′(x)-(x)>0,由此想到构造辅助函数g(x)=
变形为xf′(x)-(x)>0,由此想到构造辅助函数g(x)=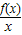 ,利用导数分析出该函数的单调性,从而得到要选择的结论.
,利用导数分析出该函数的单调性,从而得到要选择的结论.
解答:解:f(x)在(0,+∞)上是单调递增函数,故f′(x)>0在(0,+∞)上恒成立,
所以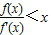 可化成xf′(x)-(x)>0
可化成xf′(x)-(x)>0
设g(x)=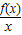 ,
,
得到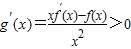 .
.
所以g(x)在(0,+∞)上单调递增.
故g(3)>g(2),即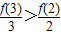 .
.
即2f(3)>3f(2).
故选D.
点评:本题考查了利用导数研究函数的单调性,解答的关键在于正确构造函数g(x)=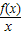 并能熟练掌握商的求导法则,是中档题.
并能熟练掌握商的求导法则,是中档题.
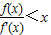 变形为xf′(x)-(x)>0,由此想到构造辅助函数g(x)=
变形为xf′(x)-(x)>0,由此想到构造辅助函数g(x)=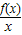 ,利用导数分析出该函数的单调性,从而得到要选择的结论.
,利用导数分析出该函数的单调性,从而得到要选择的结论.解答:解:f(x)在(0,+∞)上是单调递增函数,故f′(x)>0在(0,+∞)上恒成立,
所以
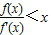 可化成xf′(x)-(x)>0
可化成xf′(x)-(x)>0设g(x)=
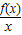 ,
,得到
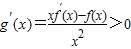 .
.所以g(x)在(0,+∞)上单调递增.
故g(3)>g(2),即
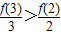 .
.即2f(3)>3f(2).
故选D.
点评:本题考查了利用导数研究函数的单调性,解答的关键在于正确构造函数g(x)=
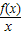 并能熟练掌握商的求导法则,是中档题.
并能熟练掌握商的求导法则,是中档题. 
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知定义在(0,1)上的函数f(x),对任意的m,n∈(1,+∞)且m<n时,都有f(
)-f(
)=f(
)记an=f(
),n∈N*,则在数列{an}中,a1+a2+…a8=( )
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
| 1 |
| n2+5n+5 |
A、f(
| ||
B、f(
| ||
C、f(
| ||
D、f(
|