题目内容

某同学在研究函数f(x)=x2ex的性质时,得到如下结论:

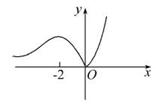
①f(x)的单调递增区间是(0,+∞);

②f(x)在x=0处取极小值,在x=-2处取极大值;

③f(x)有最小值,无最大值;

④f(x)的图象与它在(0,0)处的切线有两个交点;

⑤当m>1时,f(x)的图象与直线x=m只有一个交点.

其中正确结论的序号是　　　　.

(把你认为正确结论的序号都填上)

:②③⑤

f′(x)=2xex+x2ex=xex(2+x),

由f′(x)=0得x=0或x=-2,

所以当x∈(-∞,-2),f′(x)>0,f(x)为增函数,

当x∈(-2,0),f′(x)<0,f(x)为减函数,

当x∈(0,+∞),f′(x)>0,f(x)为增函数,可画出大致图象,故②③⑤正确.

答案

练习册系列答案
相关题目
某同学在研究函数f（x）=
x1+|x|
（x∈R）时，分别给出下面几个结论：
①f（-x）+f（x）=0在x∈R时恒成立；
②函数f（x）的值域为（-1，1）；
③若x1≠x2，则一定有f（x1）≠f（x2）；
④函数g（x）=f（x）-x在R上有三个零点．
其中正确结论的序号有
 
．
某同学在研究函数 f （x）=
x1+|x|
（x∈R） 时，分别给出下面几个结论：
①等式f（-x）+f（x）=0在x∈R时恒成立；
②函数 f （x） 的值域为 （-1，1）；
③若x1≠x2，则一定有f （x1）≠f （x2）；
④方程f（x）-x=0有三个实数根．
其中正确结论的序号有
①②③
①②③
．（请将你认为正确的结论的序号都填上）
某同学在研究函数f(x)=
x
1+|x|
（x∈R）时，给出了下面几个结论：
①函数f（x）的值域为（-1，1）；②若f（x1）=f（x2），则恒有x1=x2；③f（x）在（-∞，0）上是减函数；
④若规定f1（x）=f（x），fn+1（x）=f[fn（x）]，则fn(x)=
x
1+n|x|
对任意n∈N*恒成立，
上述结论中所有正确的结论是（　　）
某同学在研究函数f(x)=
2x|x|+1
(x∈R)时，分别得出如下几个结论：
①等式f（-x）+f（x）=0在x∈R时恒成立；
②函数f（x）的值域为（-2，2）；
③若x1≠x2，则一定有f（x1）≠f（x2）；
④函数y（x）=f（x）-2x在R上有三个零点．
其中正确的序号有
①②③
①②③
．
（2009•上海模拟）某同学在研究函数f(x)=
x1+|x|
 (x∈R)时，分别给出下面几个结论：
①等式f（-x）+f（x）=0对x∈R恒成立；
②若f（x1）≠f（x2），则一定有x1≠x2；
③若m＞0，方程|f（x）|=m有两个不等实数根；
④函数g（x）=f（x）-x在R上有三个零点．
其中正确结论的序号有
①②
①②
．（请将你认为正确的结论的序号都填上）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网