题目内容
某同学在研究函数 f （x）=
（x∈R） 时，分别给出下面几个结论：
①等式f（-x）+f（x）=0在x∈R时恒成立；
②函数 f （x） 的值域为 （-1，1）；
③若x1≠x2，则一定有f （x1）≠f （x2）；
④方程f（x）-x=0有三个实数根．
其中正确结论的序号有
| x | 1+|x| |
①等式f（-x）+f（x）=0在x∈R时恒成立；
②函数 f （x） 的值域为 （-1，1）；
③若x1≠x2，则一定有f （x1）≠f （x2）；
④方程f（x）-x=0有三个实数根．
其中正确结论的序号有
①②③
①②③
．（请将你认为正确的结论的序号都填上）分析：由奇偶性的定义来判断①，由分类讨论结合反比例函数的单调性求解②；由②结合①对称区间上的单调性相同说明③正确；由数形结合来说明④不正确．
解答：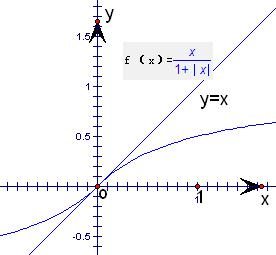
解：①f(-x)=
=-f(x)∴正确
②当x＞0时，f（x）=
∈（0，1）
由①知当x＜0时，f（x）∈（-1，0）
x=0时，f（x）=0
∴f（x）∈（-1，1）正确；
③则当x＞0时，f（x）=
反比例函数的单调性可知，f（x）在（0，+∞）上是增函数
再由①知f（x）在（-∞，0）上也是增函数，正确
④由③知f（x）的图象与y=x只有一个交点（0，0）．
不正确．
故答案为：①②③．
解：①f(-x)=| -x |
| 1+|x| |
②当x＞0时，f（x）=
| 1 | ||
1+
|
由①知当x＜0时，f（x）∈（-1，0）
x=0时，f（x）=0
∴f（x）∈（-1，1）正确；
③则当x＞0时，f（x）=
| 1 | ||
1+
|
再由①知f（x）在（-∞，0）上也是增函数，正确
④由③知f（x）的图象与y=x只有一个交点（0，0）．
不正确．
故答案为：①②③．
点评：本小题主要考查函数单调性的应用、函数奇偶性的应用、根的存在性及根的个数判断等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目