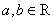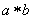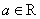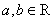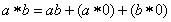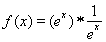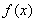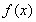题目内容
定义一种运算“*”对于正整数满足以下运算性质:
(1)2*2006=1;(2)(2n+2)*2006=3•[(2n)*2006],则2008*2006的值是
(1)2*2006=1;(2)(2n+2)*2006=3•[(2n)*2006],则2008*2006的值是
31003
31003
.分析:设(2n)*2006=an,则(2n+2)*2006=an+1,且a1=1,由此知an+1=3an,即(2n)*2006=3n-1,由此能求出2008*2006的值.
解答:解:设(2n)*2006=an,
则(2n+2)*2006=an+1,且a1=1,
∴an+1=3an,
∴an=3n-1,
即(2n)*2006=3n-1,
∴2008*2006=31003.
故答案为:31003.
则(2n+2)*2006=an+1,且a1=1,
∴an+1=3an,
∴an=3n-1,
即(2n)*2006=3n-1,
∴2008*2006=31003.
故答案为:31003.
点评:本题考查运算“*”对于正整数满足的运算性质,解题时要正确理解新定义,合理地运用新定义的性质求解.

练习册系列答案
相关题目