题目内容
已知函数f(x)=(1)求f(x)及f-1(x)的解析式;
(2)若当x∈(-1,1)时,不等式f-1(x)≥log2![]() 恒成立,试求m的取值范围.
恒成立,试求m的取值范围.
解析:(1)∵f(x)= ![]() 是奇函数,
是奇函数,
∴f(x)+f(-x)=0,
即![]() +
+![]() =
=![]() =a-1=0.
=a-1=0.
∴a=1,∴f(x)=![]() .
.
设y=![]() ,则(2x+1)y=2x-1,
,则(2x+1)y=2x-1,
∴2x=![]() ,x=log2
,x=log2![]() .
.
令![]() >0得-1<y<1,
>0得-1<y<1,
∴f(x)的反函数为y=f-1(x)=log2![]() ,x∈(-1,1).
,x∈(-1,1).
(2)∵当x∈(-1,1)时,f-1(x)≥log2![]() 恒成立,即log2
恒成立,即log2![]() ≥log2
≥log2![]() ,
,
∴![]() ≥
≥![]() .∵x∈(-1,1),
.∵x∈(-1,1),
∴1+x>0,1-x>0,m>0.
∴m≥1-x.当x∈(-1,1)时,1-x的取值集合为(0,2),∴m≥2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
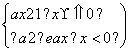 为R上的单调函数,则实数a的取值范围是 ( )
为R上的单调函数,则实数a的取值范围是 ( ) 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为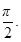
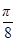 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.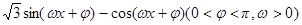 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
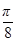 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.