题目内容
已知 为奇函数,且当
为奇函数,且当 时,
时, .当
.当 时,
时, 的最大值为
的最大值为 ,最小值为
,最小值为 ,求
,求 的值.
的值.
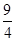 .
.
解析试题分析:要求 的值,必须求出最大值为
的值,必须求出最大值为 ,最小值为
,最小值为 ,一般应该先求出当
,一般应该先求出当 时,
时, 的表达式,而
的表达式,而 为奇函数,又当
为奇函数,又当 时,
时, ,故我们可利用奇函数的定义,当
,故我们可利用奇函数的定义,当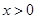 时,
时,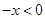 ,
, ,
,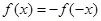 ,故可求出当
,故可求出当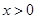 时
时 的表达式.
的表达式.
试题解析:解 ∵ 时,
时, ,且
,且 是奇函数,
是奇函数,
∴当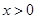 时,
时,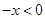 ,则
,则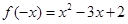 .
.
故当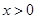 时,
时,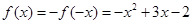 .
.
∴当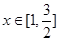 时,
时, 是增函数;
是增函数;
当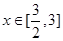 时,
时, 是减函数.
是减函数.
因此当 时,
时,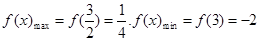 .
.
∴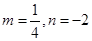 ,从而
,从而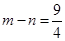 .
.
考点:函数的解析式与二次函数在给定区间上的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
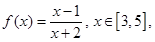
 的单调性,并证明;
的单调性,并证明; ,其中常数
,其中常数 满足
满足
 ,判断函数
,判断函数 的单调性;
的单调性; ,求
,求 时的
时的 的取值范围.
的取值范围.
 在
在 上的最大值与最小值之和为
上的最大值与最小值之和为 ,记
,记 .
. 的值;
的值; ;
; 的值.
的值. 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.
 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域; ,满足
,满足 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根. 的解析式;
的解析式;
 时,求函数
时,求函数 的表达式.
的表达式. 是奇函数
是奇函数 上单调递增,求实数a的取值范围
上单调递增,求实数a的取值范围 ,且
,且 .
. 的值;
的值; .
.
 时,求函数
时,求函数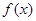 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最大值.
上的最大值.