题目内容
已知函数
 在
在 上的最大值与最小值之和为
上的最大值与最小值之和为 ,记
,记 .
.
(1)求 的值;
的值;
(2)证明 ;
;
(3)求 的值.
的值.
(1)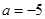 ;(2)证明见试题解析;(3)1006.
;(2)证明见试题解析;(3)1006.
解析试题分析:(1)函数 (
(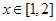 )在
)在 时,最大值为
时,最大值为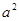 ,最小值为
,最小值为 ,在
,在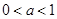 时,最大值为
时,最大值为 ,最小值为
,最小值为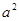 ,所以它们的和为
,所以它们的和为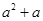 ;(2)关键是
;(2)关键是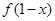 的化简,
的化简,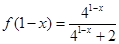
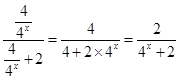 ,这样应有
,这样应有 ;(3)这种题型不可能直接计算,应该是寻找规律,由(2)的结论知函数值的计算需要配对进行,即
;(3)这种题型不可能直接计算,应该是寻找规律,由(2)的结论知函数值的计算需要配对进行,即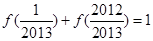 ,
, ,……,从而很快计算出结果.
,……,从而很快计算出结果.
试题解析:解(1)函数 (
(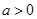 且
且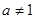 )在
)在 的最大值与最小值之和为20,
的最大值与最小值之和为20,
∴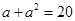 ,得
,得 ,或
,或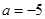 (舍去).
(舍去).
∴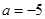 .
.
(2)∵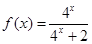
∴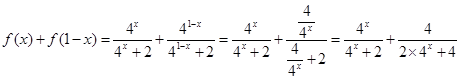
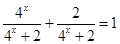 .
.
(3)由(2)知,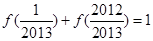 ,
, ,……,
,……,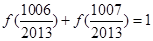 ,
,
∴原式=1006.
考点:1、函数的单调性;2、指数的运算;3、分组求和.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
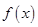 对任意
对任意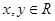 ,都有
,都有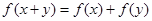 ,当
,当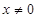 时,
时,
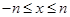 时
时  ,
,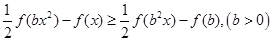
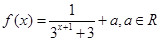
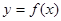 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;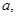 使函数
使函数
 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3),(1)求实数
的图像经过点(1,3),(1)求实数 的值;(2)求函数
的值;(2)求函数 的定义域为
的定义域为 ,并且满足
,并且满足 ,且
,且 ,当
,当 时,
时,
 的值;(3分)
的值;(3分) 的奇偶性;(3分)
的奇偶性;(3分) ,求
,求 的取值范围.(6分)
的取值范围.(6分) 直线AM,BM相交于点M,且
直线AM,BM相交于点M,且 .
. 的方程;
的方程; ,求直线PQ的方程.
,求直线PQ的方程. 为奇函数,且当
为奇函数,且当 时,
时, .当
.当 时,
时, ,最小值为
,最小值为 ,求
,求 的值.
的值. ,是否存在实数a、b、c,使
,是否存在实数a、b、c,使 同时满足下列三个条件:(1)定义域为R的奇函数;(2)在
同时满足下列三个条件:(1)定义域为R的奇函数;(2)在 上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由. ,其中
,其中
 ,当
,当 时,
时, ,求实数
,求实数 的取值集合;
的取值集合; 时,
时, 的值为负,求
的值为负,求 的取值范围.
的取值范围.