题目内容

由半椭圆
x2
a2
+
y2
b2
=1（x≥0）与半椭圆
x2
b2
+
y2
c2
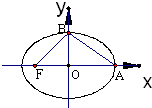
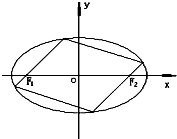
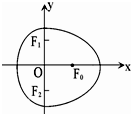
=1（x≤0）合成的曲线称作“果圆”，如图所示，其中a2=b2+c2，a＞b＞c＞0．由右椭圆
x2
a2
+
y2
b2
=1（x≥0）的焦点F0和左椭圆
x2
b2
+
y2
c2
=1（x≤0）的焦点F1，F2确定的△F0F1F2叫做果圆的焦点三角形，若果圆的焦点三角形为锐角三角形，则右椭圆
x2
a2
+
y2
b2
=1（x≥0）的离心率的取值范围为（　　）
A．(
1
3
，1)		B．(
2
3
，1)		C．(
3
3
，1)		D．(0，
3
3
)

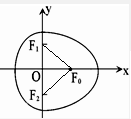
连结F0F1、F0F2，
根据“果圆”关于x轴对称，可得△F1F0F2是以F1F2为底面的等腰三角形，
∵△F0F1F2是锐角三角形，
∴等腰△F0F1F2的顶角为锐角，即∠F1F0F2∈（0，
π
2
）．
由此可得|0F0|＞|0F1|，
∵|0F0|、|0F1|分别是椭圆
x2
a2
+
y2
b2
=1、
x2
b2
+
y2
c2
=1的半焦距，
∴c＞
b2-c2
，平方得c2＞b2-c2，
又∵b2=a2-c2，∴c2＞a2-2c2，解得3c2＞a2，
两边都除以a2，得3•(
c
a
)2＞1，解之得
c
a
＞
3
3
．
∵右椭圆
x2
a2
+
y2
b2
=1（x≥0）的离心率e=
c
a
∈（0，1），
∴所求离心率e的范围为（
3
3
，1）．
故选：C
练习册系列答案
相关题目
已知椭圆方程为
x2
16
+
y2
m2
=1(m＞0)，直线y=
2
2
x与该椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点，则m的值为______．
椭圆的一个焦点到相应准线的距离为
5
4
，离心率为
2
3
，则椭圆的短轴长为（　　）
A．
5
2
B．4
5
C．2
5
D．
5
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
2
2
，左、右焦点分别是F1，F2，过点F1的直线l交C于A，B两点，且△ABF2的周长为4
2
．则椭圆C的方程为______．
如图，椭圆中心在坐标原点，F为左焦点，当
FB
⊥
AB
时，其离心率为
5
-1
2
，此类椭圆被称为“黄金椭圆”，类比“黄金椭圆”，可推算出“黄金双曲线”的离心率为（　　）
A．
5
+1
2
B．
5
-1
2
C．
5
+1		D．
5
-1
已知椭圆E：
x2
4
+y2=1，椭圆E的内接平行四边形的一组对边分别经过它的两个焦点（如图），则这个平行四边形面积的最大值是______．
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上任意一点到两焦点的距离分别为d1，d2，焦距为2c，若d1，2c，d2成等差数列，则椭圆的离心率为（　　）
A．
1
2
B．
2
2
C．
3
2
D．
3
4
设直线l过点P（0，3），和椭圆
x2
9
+
y2
4
=1顺次交于A、B两点，则
AP
PB
的取值范围是______．
【文科】已知点A，B是椭圆
x2
m2
+
y2
n2
=1（m＞0，n＞0）上两点，且
AO
=λ
BO
，则λ=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网