题目内容
12.求下列双曲线的实轴长,虚轴长,焦点坐标,顶点坐标,离心率与渐近线方程,并用“描点法”画出图形.(1)9x2-y2=81;
(2)$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{4}$=1.
分析 双曲线方程化为标准方程,确定几何量,即可求出双曲线的实轴长,虚轴长,焦点坐标,顶点坐标,离心率与渐近线方程.
解答 解:(1)9x2-y2=81可化为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{81}$=1,∴a=3,b=9,c=3$\sqrt{10}$,
∴实轴长为6,虚轴长18,焦点坐标(±3$\sqrt{10}$,0),顶点坐标(±3,0),离心率$\sqrt{10}$,渐近线方程y=±3x;
如图所示
(2)$\frac{{y}^{2}}{2}-\frac{{x}^{2}}{4}$=1,a=$\sqrt{2}$,b=2,c=$\sqrt{6}$,
∴实轴长为2$\sqrt{2}$,虚轴长4,焦点坐标(0,±$\sqrt{6}$),顶点坐标(0,±$\sqrt{2}$),离心率$\sqrt{3}$,渐近线方程y=±$\sqrt{2}$x.如图所示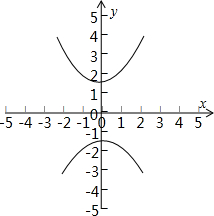
点评 本题考查双曲线的方程与性质,考查学生的作图能力,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
4.不等式|x一2|≤5的解集为( )
| A. | [-5,5] | B. | (-2,5) | C. | [-3,7] | D. | R |
2.函数f(x)=log${\;}_{\frac{1}{3}}$(5-4x-x2)的值域为( )
| A. | [2,+∞) | B. | (-∞,-2] | C. | [-2,+∞) | D. | (-∞,2] |