题目内容
(本题满分14分)
对数列{an},规定{△an}为数列{an}的一阶差分数列,其中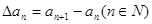 。
。
对自然数k,规定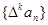 为{an}的k阶差分数列,其中
为{an}的k阶差分数列,其中 。
。
(1)已知数列{an}的通项公式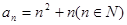 ,试判断
,试判断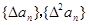 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列{an}首项a1=1,且满足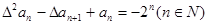 ,求数列{an}的通项公式。
,求数列{an}的通项公式。
(3)对(2)中数列{an},是否存在等差数列{bn},使得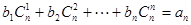 对一切自然
对一切自然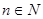 都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
都成立?若存在,求数列{bn}的通项公式;若不存在,则请说明理由。
(1)根据给定的新定义来分析得到结论。
(2)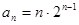
(3)存在等差数列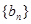 ,bn=n,使得
,bn=n,使得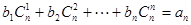 对一切自然
对一切自然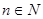 都成立。
都成立。
解析试题分析:解:(1)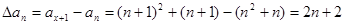
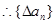 是首项为4,公差为2的等差数列
是首项为4,公差为2的等差数列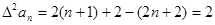
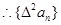 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列
(2)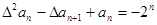 ,即
,即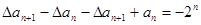 ,即
,即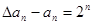
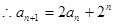
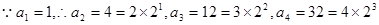
猜想: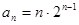
证明:i)当n=1时,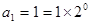 ;
;
ii)假设n=k时,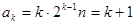 时,
时,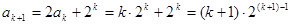 结论也成立
结论也成立
∴由i)、ii)可知,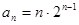
(3)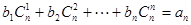 ,即
,即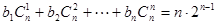
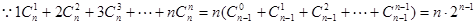
∴存在等差数列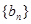 ,bn=n,使得
,bn=n,使得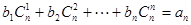 对一切自然
对一切自然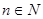 都成立。
都成立。
考点:数列的新定义,以及等差数列和求和的综合
点评:解决该试题的关键是利用数列的定义以及等差数列的概念结合得到结论,属于基础题。

练习册系列答案
相关题目
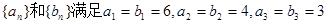 ,且数列
,且数列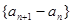 是等差数列,
是等差数列,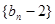 是等比数列.
是等比数列. 的通项公式;
的通项公式; 的前
的前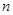 项和为
项和为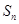 ,求
,求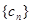 满足
满足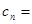
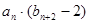 ,求数列
,求数列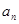 }中,a1=3,
}中,a1=3,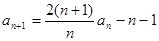 ,
,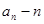 关于n的表达式(不用证明);
关于n的表达式(不用证明);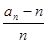 }是什么类型的数列并证明;
}是什么类型的数列并证明; }的前n项和为
}的前n项和为 ,且
,且 =1,
=1,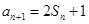 ,数列{
,数列{ }满足
}满足 ,点P(
,点P( )在直线x―y+2=0上,
)在直线x―y+2=0上, .
. ,求数列{
,求数列{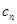 }的前n项和
}的前n项和 .
.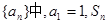 是数列
是数列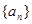 的前n项和,对任意
的前n项和,对任意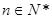 ,有2Sn=2
,有2Sn=2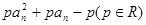 .
.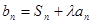 ,(
,(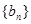 从第二项起每一项都比它的前一项大,求
从第二项起每一项都比它的前一项大,求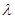 的取值范围.
的取值范围.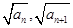 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点(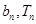 )在直线y=-
)在直线y=-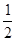 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。 的相邻两项
的相邻两项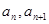 是关于
是关于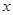 的方程
的方程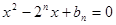
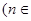 N
N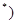 的两根,且
的两根,且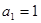 .
.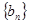 的通项公式;
的通项公式; 是数列
是数列 项和, 问是否存在常数
项和, 问是否存在常数 ,使得
,使得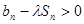 对任意
对任意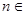 N
N 都成立,若存在, 求出
都成立,若存在, 求出 前
前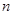 项和
项和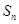 满足
满足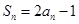 ,等差数列
,等差数列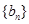 满足
满足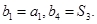
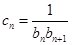 ,数列
,数列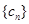 的前
的前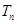 ,问
,问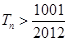 的最小正整数n是多少?
的最小正整数n是多少?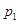 ,恰好
,恰好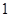 次正面向上的概率为
次正面向上的概率为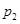 ;等比数列
;等比数列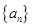 满足:
满足: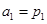 ,
,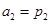
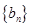 满足:
满足: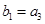 ,
,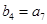 ,求等差数列
,求等差数列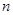 项和
项和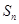 .
.