题目内容
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一点,且
上一点,且![]() ,
,![]() .
.
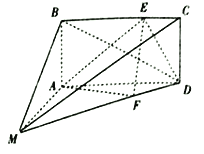
(1)证明:![]() ;
;
(2)证明:![]() 平面
平面![]() ,并求三棱锥
,并求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析; (2)1.
【解析】
(1)推导出AM⊥AD,从而AM⊥平面ABCD,由此能证明AM⊥BD;(2)推导出CE=ND,BC∥AD,EN∥AB,FN∥AM,从而平面ENF∥平面MAB,进而EF∥平面MAB,由VD﹣AEF=VF﹣ADE,能求出三棱锥D﹣AEF的体积.
(1)∵AM=AD=3,MD=3![]() ,
,
∴AM2+AD2=MD2,∴AM⊥AD,
∵平面MAD⊥平面ABCD,平面MAD∩平面ABCD=AD,
∴AM⊥平面ABCD,
又BD平面ABCD,∴AM⊥BD.
(2)在棱AD上取一点N,使得ND=1,

∵CE=1,∴CE=ND,又BC∥AD,
∴EC![]() ND,又AB∥CD,∴EN∥AB,
ND,又AB∥CD,∴EN∥AB,
∵![]() =
=![]() ,∴FN∥AM,
,∴FN∥AM,
∵FN∩EN=N,∴平面ENF∥平面MAB,又EF平面ENF,
∴EF∥平面MAB,
∵AM⊥平面ABCD,且FD=![]() MD,AM=3,
MD,AM=3,
∴F到平面ABCD的距离d=![]() ,
,
∴VD﹣AEF=VF﹣ADE=![]() =1.
=1.

练习册系列答案
相关题目
【题目】为普及学生安全逃生知识与安全防护能力,某学校高一年级举办了安全知识与安全逃生能力竞赛,该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛,现将所有参赛选手参加笔试的成绩(得分均为整数,满分为![]() 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
分数(分数段) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)求表中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)按规定,预赛成绩不低于![]() 分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为
分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

