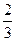题目内容
假设你家订了一份报纸,送报人可能在早上6:30~7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00~8:00之间,现在利用随机模拟试验的方法,设送报人送到的时间为 ,你父亲去上班的时间为
,你父亲去上班的时间为 ,通过计算机产生如下20组数据,根据这20组数据,求你父亲在离开家前能得到报纸的概率是多少?
,通过计算机产生如下20组数据,根据这20组数据,求你父亲在离开家前能得到报纸的概率是多少?
 ,你父亲去上班的时间为
,你父亲去上班的时间为 ,通过计算机产生如下20组数据,根据这20组数据,求你父亲在离开家前能得到报纸的概率是多少?
,通过计算机产生如下20组数据,根据这20组数据,求你父亲在离开家前能得到报纸的概率是多少?| 序号 | x的值 | y的值 |
| 1 | 6.9877 | 7.8705 |
| 2 | 7.4551 | 7.8306 |
| 3 | 7.2142 | 7.1536 |
| 4 | 7.1956 | 7.8930 |
| 5 | 7.3802 | 7.3392 |
| 6 | 7.1752 | 7.6632 |
| 7 | 6.9864 | 7.5624 |
| 8 | 6.9376 | 7.8601 |
| 9 | 6.7595 | 7.7660 |
| 10 | 6.8464 | 7.3132 |
| 11 | 7.4267 | 7.7279 |
| 12 | 6.9119 | 7.4720 |
| 13 | 6.5753 | 7.2793 |
| 14 | 7.0090 | 7.7624 |
| 15 | 7.4258 | 7.4488 |
| 16 | 7.3529 | 7.2884 |
| 17 | 7.0754 | 7.8694 |
| 18 | 7.2386 | 7.2847 |
| 19 | 7.1166 | 7.8057 |
| 20 | 7.4023 | 7.3700 |

解本题的关键是使父亲在离开家前能得到报纸,则须满足x≤y.
要使父亲在离开家前能得到报纸,则x≤y,从20组随机数中可以看出有16组满足,所以父亲离开家前能得到报纸的概率
要使父亲在离开家前能得到报纸,则x≤y,从20组随机数中可以看出有16组满足,所以父亲离开家前能得到报纸的概率


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
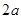 的正方形及其内切圆,随机向正方形内丢一粒豆子,则豆子落入圆内的概率是 ;
的正方形及其内切圆,随机向正方形内丢一粒豆子,则豆子落入圆内的概率是 ;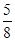
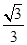

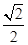



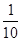
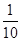
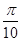
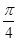
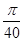
 的圆依次相切,右边正方形内有一个半径为a的内切圆,在这两个图形上各随机撒一粒黄豆,落在阴影内的概率分别为
的圆依次相切,右边正方形内有一个半径为a的内切圆,在这两个图形上各随机撒一粒黄豆,落在阴影内的概率分别为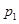 ,
, ,则
,则
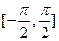 上随机取一个数x,
上随机取一个数x,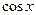 的值介于0到
的值介于0到 之 间的概率为
之 间的概率为  ( ).
( ).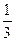 B
B .
. C.
C.