题目内容
△ABC中,三个内角A、B、C所对的边分别为a、b、c,若B=60°,a=( -1)c.
-1)c.
(1)求角A的大小;
(2)已知S△ABC=6+2 ,求函数f(x)=cos2x+asinx的最大值.
,求函数f(x)=cos2x+asinx的最大值.
解:(1)因为B=60°,所以A+C=120°,C=120°-A
因为a=( -1)c,由正弦定理可得:sinA=(
-1)c,由正弦定理可得:sinA=(  )sin C
)sin C
sinA=( )sin(
)sin(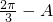 )=(
)=( )(sin
)(sin cosA-cos
cosA-cos sinA)=(
sinA)=( )(
)( cosA+
cosA+ sinA),
sinA),
整理可得:tanA=1 所以,A=45°(或 )
)
(2)因为 S△ABC=6+2 ,所以
,所以 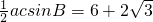 即
即 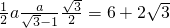
所以a=4
函数f(x)=cos2x+4sinx=1-2sin2x+4sinx=-2(sinx-1)2+3
∴当 sinx=1时,fmax(x)=3,
分析:(1)利用正弦定理,以及三角形的内角和,直接求出角A的大小;
(2)利用S△ABC=6+2 ,求出a,然后化简函数f(x)=cos2x+asinx为一个角的一个三角函数的形式,然后求出它的最大值.
,求出a,然后化简函数f(x)=cos2x+asinx为一个角的一个三角函数的形式,然后求出它的最大值.
点评:本题是中档题,考查正弦定理的应用,三角函数值域及二次函数值域,容易忽视正弦函数的范围而出错.高考对三角函数的考查一直以中档题为主,只要认真运算即可
因为a=(
 -1)c,由正弦定理可得:sinA=(
-1)c,由正弦定理可得:sinA=(  )sin C
)sin CsinA=(
 )sin(
)sin(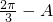 )=(
)=( )(sin
)(sin cosA-cos
cosA-cos sinA)=(
sinA)=( )(
)( cosA+
cosA+ sinA),
sinA),整理可得:tanA=1 所以,A=45°(或
 )
) (2)因为 S△ABC=6+2
 ,所以
,所以 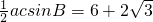 即
即 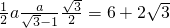
所以a=4
函数f(x)=cos2x+4sinx=1-2sin2x+4sinx=-2(sinx-1)2+3
∴当 sinx=1时,fmax(x)=3,
分析:(1)利用正弦定理,以及三角形的内角和,直接求出角A的大小;
(2)利用S△ABC=6+2
 ,求出a,然后化简函数f(x)=cos2x+asinx为一个角的一个三角函数的形式,然后求出它的最大值.
,求出a,然后化简函数f(x)=cos2x+asinx为一个角的一个三角函数的形式,然后求出它的最大值.点评:本题是中档题,考查正弦定理的应用,三角函数值域及二次函数值域,容易忽视正弦函数的范围而出错.高考对三角函数的考查一直以中档题为主,只要认真运算即可

练习册系列答案
相关题目