题目内容
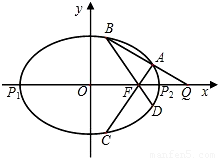
 如图,已知椭圆E:
如图,已知椭圆E:| x2 |
| 100 |
| y2 |
| 25 |
(1)若点P的坐标为(6,4),求四边形ABCP的面积;
(2)若四边形ABCP为梯形,求点P的坐标;
(3)若
| BP |
| BA |
| BC |
分析:(1)先求B、C的坐标,再利用四边形ABCP的面积为三角形与梯形面积的和,即可得到结论;
(2)因为ABCP为梯形分情况讨论:①AP平行与BC;②AB平行于CP,则kAB=kCP,求出直线CP的方程,与椭圆方程联立,即可求得P的坐标;
(3)设P(x,y),根据
=m•
+n•
(m,n为实数),可得x=6m+12n-6,y=9m-4,进而可得m+n,利用三角换元,可求m+n的最大值.
(2)因为ABCP为梯形分情况讨论:①AP平行与BC;②AB平行于CP,则kAB=kCP,求出直线CP的方程,与椭圆方程联立,即可求得P的坐标;
(3)设P(x,y),根据
| BP |
| BA |
| BC |
解答:解:(1)将y=-4代入椭圆E:
+
=1,可得x=±6,∴B(-6,-4),C(6,-4)
∴四边形ABCP的面积为三角形与梯形面积的和
∴S四边形ABCP=
+
=78
(2)因为ABCP为梯形分情况讨论
①AP平行与BC,则y=5与A重合,所以舍;
②AB平行于CP,则kAB=
=
=kCP,
设直线CP的方程为y=
x+C,代入(6,-4)可得C=-13
∴直线CP的方程为y=
x-13,
与椭圆E:
+
=1,联立消元可得5x2-78x+288=0
∴x=6或
代入直线CP的方程为y=
x-13,可得y=-4或
∴P(
,
);
(3)设P(x,y),∵
=m•
+n•
(m,n为实数),
∴(x+6,y+4)=m(6,9)+n(12,0)=(6m+12n,9m)
∴x=6m+12n-6,y=9m-4
∴m=
y+
,n=
x-
+
∴m+n=
令x=10cosθ,y=5sinθ,∴m+n=
cosθ-
sinθ+
=
cos(θ+α)+
,所以最大值为
+
,
∴m+n的最大值为
+
.
| x2 |
| 100 |
| y2 |
| 25 |
∴四边形ABCP的面积为三角形与梯形面积的和
∴S四边形ABCP=
| 6×(4+5) |
| 2 |
| 6×(8+9) |
| 2 |
(2)因为ABCP为梯形分情况讨论
①AP平行与BC,则y=5与A重合,所以舍;
②AB平行于CP,则kAB=
| 5-(-4) |
| 0-(-6) |
| 3 |
| 2 |
设直线CP的方程为y=
| 3 |
| 2 |
∴直线CP的方程为y=
| 3 |
| 2 |
与椭圆E:
| x2 |
| 100 |
| y2 |
| 25 |
∴x=6或
| 48 |
| 5 |
代入直线CP的方程为y=
| 3 |
| 2 |
| 7 |
| 5 |
∴P(
| 48 |
| 5 |
| 7 |
| 5 |
(3)设P(x,y),∵
| BP |
| BA |
| BC |
∴(x+6,y+4)=m(6,9)+n(12,0)=(6m+12n,9m)
∴x=6m+12n-6,y=9m-4
∴m=
| 1 |
| 9 |
| 4 |
| 9 |
| 1 |
| 12 |
| y |
| 18 |
| 5 |
| 18 |
∴m+n=
| 3x-2y+26 |
| 36 |
令x=10cosθ,y=5sinθ,∴m+n=
| 5 |
| 6 |
| 5 |
| 18 |
| 13 |
| 18 |
5
| ||
| 18 |
| 13 |
| 18 |
5
| ||
| 18 |
| 13 |
| 18 |
∴m+n的最大值为
5
| ||
| 18 |
| 13 |
| 18 |
点评:本题考查四边形面积的计算,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是确定坐标之间的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
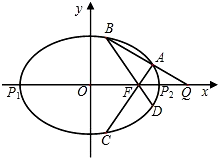 (2013•宁波二模)如图,已知椭圆E:
(2013•宁波二模)如图,已知椭圆E:




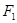 、
、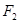 在x轴上,离心率
在x轴上,离心率
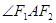 的角平分线所在直线
的角平分线所在直线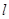 的方程.
的方程.
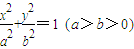 的离心率是
的离心率是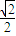 ,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足
,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足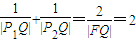 .
.