题目内容
如图,已知椭圆E: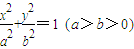 的离心率是
的离心率是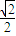 ,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足
,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足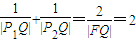 .
.(Ⅰ) 求椭圆E的方程以及点Q的坐标;
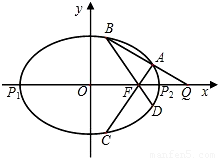
(Ⅱ) 过点Q的动直线l交椭圆E于A、B两点,连结AF并延长交椭圆于点C,连结BF并延长交椭圆于点D.
①求证:B、C关于x轴对称;
②当四边形ABCD的面积取得最大值时,求直线l的方程.
【答案】分析:(Ⅰ)设点F(c,0),Q(x,0)(x>a),由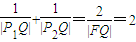 ,得
,得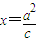 ,依题意|FQ|=1,即
,依题意|FQ|=1,即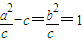 ,再由离心率
,再由离心率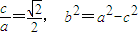 ,联立即可解得a,b,c,及点Q坐标;
,联立即可解得a,b,c,及点Q坐标;
(Ⅱ)①设直线l的方程为x=my+2,代入椭圆E的方程可得(2+m2)y2+4my+2=0,设A(x1,y1),B(x2,y2),点B关于x轴的对称点B1(x2,-y2),只需证明B1即为点C,可证A、F、B1三点共线,根据斜率相等及韦达定理即可证明;②由①得B、C关于x轴对称,同理A、D关于x轴对称,易知四边形ABCD是一个等腰梯形,从而四边形ABCD的面积S=|x1-x2|•(|y1|+|y2|)=|m|•|y1-y2|•|y1+y2|,代入韦达定理可得关于m的函数,通过换元借助导数可求得S的最大值及相应的m值,从而可得直线方程;
解答:解:(Ⅰ)设点F(c,0),Q(x,0)(x>a).

由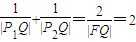 ,
,
可得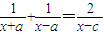 ,解得
,解得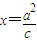 .
.
依题意|FQ|=1,即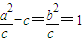 .
.
又因为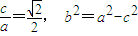 ,所以
,所以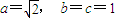 .
.
故椭圆的方程是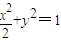 ,点Q的坐标是(2,0).
,点Q的坐标是(2,0).
(Ⅱ)①设直线l的方程为x=my+2,代入椭圆E的方程可得(2+m2)y2+4my+2=0,
依题意,△=(4m)2-8(2+m2)=8(m2-2)>0,m2>2.
设A(x1,y1),B(x2,y2),则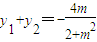 ,
,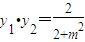 .(*)
.(*)
点B关于x轴的对称点B1(x2,-y2),
则A、F、B1三点共线等价于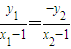
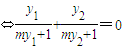
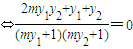 ,
,
由(*)可知上述关系成立.
因此,点C即是点B1,这说明B、C关于x轴对称.
②由①得B、C关于x轴对称,同理,A、D关于x轴对称.
所以,四边形ABCD是一个等腰梯形,
则四边形ABCD的面积S=|x1-x2|•(|y1|+|y2|)=|m|•|y1-y2|•|y1+y2|=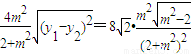 .
.
设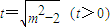 ,则m2=t2+2,
,则m2=t2+2,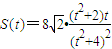 .
.
求导可得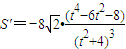 ,令S'=0,可得
,令S'=0,可得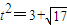 .
.
由于S(t)在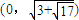 上单调增,在
上单调增,在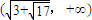 上单调减.
上单调减.
所以,当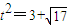 即
即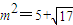 时,四边形ABCD的面积S取得最大值.
时,四边形ABCD的面积S取得最大值.
此时,直线l的方程是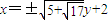 .
.
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程及直线的方程,考查三点共线及直线斜率,考查学生综合运用所学知识分析解决问题的能力,本题综合性强,所用知识点繁多,对能力要求高.
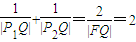 ,得
,得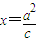 ,依题意|FQ|=1,即
,依题意|FQ|=1,即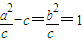 ,再由离心率
,再由离心率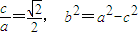 ,联立即可解得a,b,c,及点Q坐标;
,联立即可解得a,b,c,及点Q坐标;(Ⅱ)①设直线l的方程为x=my+2,代入椭圆E的方程可得(2+m2)y2+4my+2=0,设A(x1,y1),B(x2,y2),点B关于x轴的对称点B1(x2,-y2),只需证明B1即为点C,可证A、F、B1三点共线,根据斜率相等及韦达定理即可证明;②由①得B、C关于x轴对称,同理A、D关于x轴对称,易知四边形ABCD是一个等腰梯形,从而四边形ABCD的面积S=|x1-x2|•(|y1|+|y2|)=|m|•|y1-y2|•|y1+y2|,代入韦达定理可得关于m的函数,通过换元借助导数可求得S的最大值及相应的m值,从而可得直线方程;
解答:解:(Ⅰ)设点F(c,0),Q(x,0)(x>a).

由
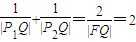 ,
,可得
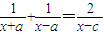 ,解得
,解得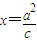 .
.依题意|FQ|=1,即
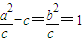 .
.又因为
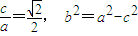 ,所以
,所以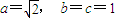 .
.故椭圆的方程是
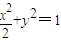 ,点Q的坐标是(2,0).
,点Q的坐标是(2,0). (Ⅱ)①设直线l的方程为x=my+2,代入椭圆E的方程可得(2+m2)y2+4my+2=0,
依题意,△=(4m)2-8(2+m2)=8(m2-2)>0,m2>2.
设A(x1,y1),B(x2,y2),则
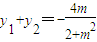 ,
,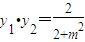 .(*)
.(*)点B关于x轴的对称点B1(x2,-y2),
则A、F、B1三点共线等价于
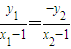
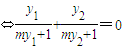
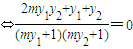 ,
,由(*)可知上述关系成立.
因此,点C即是点B1,这说明B、C关于x轴对称.
②由①得B、C关于x轴对称,同理,A、D关于x轴对称.
所以,四边形ABCD是一个等腰梯形,
则四边形ABCD的面积S=|x1-x2|•(|y1|+|y2|)=|m|•|y1-y2|•|y1+y2|=
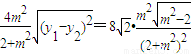 .
.设
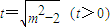 ,则m2=t2+2,
,则m2=t2+2,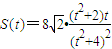 .
.求导可得
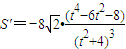 ,令S'=0,可得
,令S'=0,可得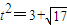 .
.由于S(t)在
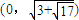 上单调增,在
上单调增,在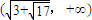 上单调减.
上单调减.所以,当
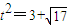 即
即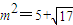 时,四边形ABCD的面积S取得最大值.
时,四边形ABCD的面积S取得最大值. 此时,直线l的方程是
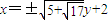 .
.点评:本题考查直线与圆锥曲线的位置关系、椭圆方程及直线的方程,考查三点共线及直线斜率,考查学生综合运用所学知识分析解决问题的能力,本题综合性强,所用知识点繁多,对能力要求高.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
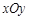 中,如图,已知椭圆E:
中,如图,已知椭圆E: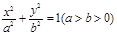 的左、右顶点分别为
的左、右顶点分别为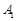 、
、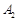 ,
,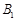 、
、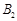 .设直线
.设直线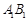 的倾斜角的正弦值为
的倾斜角的正弦值为 ,圆
,圆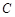 与以线段
与以线段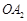 为直径的圆
为直径的圆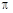 ,求圆
,求圆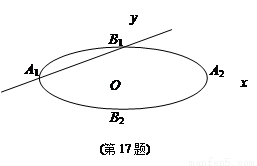
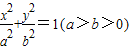 的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为
的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为 ,圆C与以线段OA2为直径的圆关于直线A1B1对称.
,圆C与以线段OA2为直径的圆关于直线A1B1对称.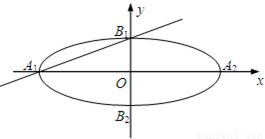
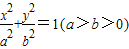 的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为
的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为 ,圆C与以线段OA2为直径的圆关于直线A1B1对称.
,圆C与以线段OA2为直径的圆关于直线A1B1对称.
 的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为
的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为 ,圆C与以线段OA2为直径的圆关于直线A1B1对称.
,圆C与以线段OA2为直径的圆关于直线A1B1对称.