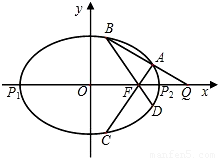
题目内容
如图,已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
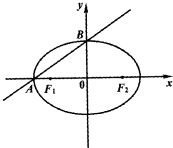
(I)求椭圆的方程;
(II)设C,D是椭圆E上两不同点,CD∥AB,直线CD与x轴、y轴分别交于M,N两点,且
| MC |
| CN |
| MD |
| DN |
分析:(I)由题意知:
,由此能求出椭圆方程.
(II)由A(-2,0),B(0,1),知kAB=
.由CD∥AB,设直线CD的方程为y=
x+m,由已知,得M(-2m,0),N(0,m),设C(x1,y1),D(x2,y2),由
,得x2+2mx+2m2-2=0,再由根的判别式和韦达定理知λ=-1-
,同理,μ=-1-
,由此能求出λ+μ∈(-∞,-2]∪(2,+∞).
|
(II)由A(-2,0),B(0,1),知kAB=
| 1 |
| 2 |
| 1 |
| 2 |
|
| 2m |
| x1 |
| 2m |
| x2 |
解答:解:(I)由题意知:
,
∴a2=4,b2=1,
∴椭圆方程为
+y2=1.
(II)∵A(-2,0),B(0,1),∴kAB=
.
由CD∥AB,设直线CD的方程为y=
x+m,
由已知,得M(-2m,0),N(0,m),
设C(x1,y1),D(x2,y2),
由
,得x2+2mx+2m2-2=0,
△=(2m)2-4(2m2-2)>0,∴m2<2,
∴x1+x2=-2m,x1x2=2m2-2,
由
=λ
得(x1+2m,y1)=λ(-x1,m-y1),
∴x1+2m=-λx1,即λ=-1-
,
同理,由
=μ
,得μ=-1-
,
∴λ+μ=-2-2m(
+
)=-2-2m×
=-2+
=
,
由m2<2,得
∈(-∞,-2]∪(2,+∞),
∴λ+μ∈(-∞,-2]∪(2,+∞).
|
∴a2=4,b2=1,
∴椭圆方程为
| x2 |
| 4 |
(II)∵A(-2,0),B(0,1),∴kAB=
| 1 |
| 2 |
由CD∥AB,设直线CD的方程为y=
| 1 |
| 2 |
由已知,得M(-2m,0),N(0,m),
设C(x1,y1),D(x2,y2),
由
|
△=(2m)2-4(2m2-2)>0,∴m2<2,
∴x1+x2=-2m,x1x2=2m2-2,
由
| MC |
| CN, |
∴x1+2m=-λx1,即λ=-1-
| 2m |
| x1 |
同理,由
| MD |
| DN |
| 2m |
| x2 |
∴λ+μ=-2-2m(
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| 2m2 |
| m2-1 |
| 2 |
| m2-1 |
由m2<2,得
| 2 |
| m2-1 |
∴λ+μ∈(-∞,-2]∪(2,+∞).
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
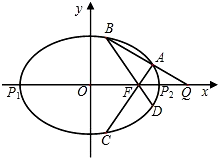 (2013•宁波二模)如图,已知椭圆E:
(2013•宁波二模)如图,已知椭圆E:




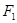 、
、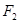 在x轴上,离心率
在x轴上,离心率
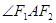 的角平分线所在直线
的角平分线所在直线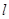 的方程.
的方程.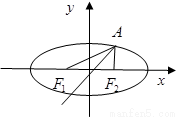
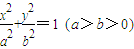 的离心率是
的离心率是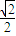 ,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足
,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足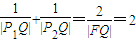 .
.