题目内容
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.

(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ,求四棱锥F—ABCD的体积.
,求四棱锥F—ABCD的体积.

(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4
 ,求四棱锥F—ABCD的体积.
,求四棱锥F—ABCD的体积.(1)见解析 (2)16

(1)证明 方法一 ∵EF∥AD,AD∥BC,∴EF∥BC.
又EF=AD=BC,∴四边形EFBC是平行四边形,
∴H为FC的中点.
又∵G是FD的中点,∴HG∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.

方法二 连接EA,∵ADEF是正方形,
∴G是AE的中点.
∴在△EAB中,GH∥AB.
又∵AB∥CD,∴GH∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.
(2)解 ∵平面ADEF⊥平面ABCD,交线为AD,
且FA⊥AD,∴FA⊥平面ABCD.
∵AD=BC=6,∴FA=AD=6.
又∵CD=2,DB=4 ,CD2+DB2=BC2,∴BD⊥CD.
,CD2+DB2=BC2,∴BD⊥CD.
∵S?ABCD=CD·BD=8 ,
,
∴VF—ABCD=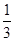 S?ABCD·FA=
S?ABCD·FA=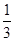 ×8
×8 ×6=16
×6=16 .
.
又EF=AD=BC,∴四边形EFBC是平行四边形,
∴H为FC的中点.
又∵G是FD的中点,∴HG∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.

方法二 连接EA,∵ADEF是正方形,
∴G是AE的中点.
∴在△EAB中,GH∥AB.
又∵AB∥CD,∴GH∥CD.
∵HG?平面CDE,CD?平面CDE,
∴GH∥平面CDE.
(2)解 ∵平面ADEF⊥平面ABCD,交线为AD,
且FA⊥AD,∴FA⊥平面ABCD.
∵AD=BC=6,∴FA=AD=6.
又∵CD=2,DB=4
 ,CD2+DB2=BC2,∴BD⊥CD.
,CD2+DB2=BC2,∴BD⊥CD.∵S?ABCD=CD·BD=8
 ,
,∴VF—ABCD=
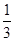 S?ABCD·FA=
S?ABCD·FA=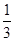 ×8
×8 ×6=16
×6=16 .
.
练习册系列答案
相关题目
 中,平面
中,平面 平面
平面 ,
, 于点
于点 ,且
,且 ,
, ,
, 

 ,
, ,求三棱锥
,求三棱锥
 的边长为
的边长为 ,点
,点 分别在边
分别在边 上,
上,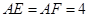 ,现将△
,现将△ 沿线段
沿线段 折起到△
折起到△ 位置,使得
位置,使得 .
.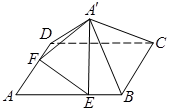
 的体积;
的体积; 的夹角.
的夹角.
 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积.

 的半圆面,则该圆锥的体积为 .
的半圆面,则该圆锥的体积为 . 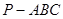 的各顶点都在一半径为
的各顶点都在一半径为 的球面上,球心
的球面上,球心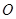 在
在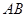 上,且有
上,且有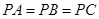 ,底面
,底面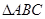 中
中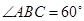 ,则球与三棱锥的体积之比是 .
,则球与三棱锥的体积之比是 .