题目内容
12.已知集合{x|(x+a)(x2+bx+c)=0}={1,2},求集合{x|(ax+1)(cx2+bx+1)=0}.分析 结合二次函数的性质求出a,b,c的值,代入(ax+1)(cx2+bx+1)=0,解方程即可.
解答 解:由集合{x|(x+a)(x2+bx+c)=0}={1,2},
x=-a=1时,$\left\{\begin{array}{l}{△{=b}^{2}-4c=0}\\{4+2b+c=0}\end{array}\right.$,解得:a=-1,b=-4,c=4,
∴{x|(ax+1)(cx2+bx+1)=0}={x|(-x+1)(4x2-4x+1)=0}={1,$\frac{1}{2}$},
x=-a=2时,$\left\{\begin{array}{l}{△{=b}^{2}-4c=0}\\{1+b+c=0}\end{array}\right.$,解得:a=-2,b=-2,c=1,
∴{x|(ax+1)(cx2+bx+1)=0}={x|(-2x+1)(x2-2x+1)=0}={1,$\frac{1}{2}$},
综上:{x|(ax+1)(cx2+bx+1)=0}={1,$\frac{1}{2}$}.
点评 本题考查了二次函数的性质,考查集合问题,是一道基础题.

练习册系列答案
相关题目
2.在△ABC中,若2cosB•sinA=sinC,则△ABC一定是( )三角形.
| A. | 等腰 | B. | 直角 | C. | 等边 | D. | 等腰直角 |
7.函数f(x)=$\left\{\begin{array}{l}{(x+a)^{2},x≤0}\\{x+\frac{1}{x}+a,x>0}\end{array}\right.$,若f(0)是f(x)的最小值,则a的取值范围为( )
| A. | [-1,0] | B. | [-1,2] | C. | [1,2] | D. | [0,2] |
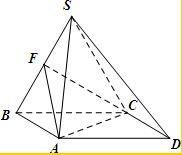 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2$\sqrt{2}$,SB=SC=AB=2,F为线段SB的中点.
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2$\sqrt{2}$,SB=SC=AB=2,F为线段SB的中点.