题目内容
已知双曲线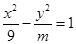 的一个焦点在圆
的一个焦点在圆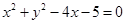 上,则双曲线的渐近线方程为
上,则双曲线的渐近线方程为
A.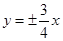 | B.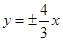 | C.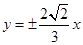 | D.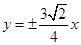 |
B
解析试题分析:用m表示在圆上的焦点坐标(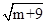 ,0),代入圆的方程,求出m的值,然后即可求出双曲线的渐近线方程.
,0),代入圆的方程,求出m的值,然后即可求出双曲线的渐近线方程.
考点:(1)双曲线的几何性质.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
抛物线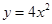 的焦点到准线的距离是( )
的焦点到准线的距离是( )
| A.2 | B.4 | C.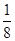 | D.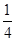 |
若双曲线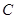 :
: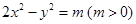 与抛物线
与抛物线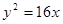 的准线交于
的准线交于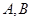 两点,且
两点,且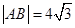 ,则
,则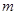 的值是( )
的值是( )
A.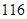 | B.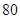 . . | C.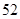 | D.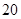 |
圆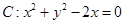 的圆心到双曲线
的圆心到双曲线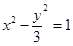 的渐近线的距离是( )
的渐近线的距离是( )
A.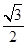 | B.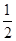 | C.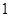 | D.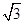 |
已知椭圆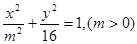 和双曲线
和双曲线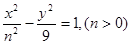 有相同的焦点
有相同的焦点 ,点
,点 为椭圆和双曲线的一个交点,则
为椭圆和双曲线的一个交点,则 的值为( )
的值为( )
| A.16 | B.25 | C.9 | D.不为定值 |
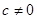 是方程
是方程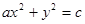 表示椭圆或双曲线的 ( )
表示椭圆或双曲线的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.不充分不必要条件 |
已知双曲线C: -
- =1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为( )
=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为( )
A.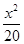 - - =1 =1 | B.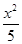 - -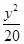 =1 =1 |
C.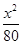 - -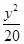 =1 =1 | D.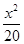 - -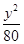 =1 =1 |
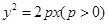 的焦点为F,斜率
的焦点为F,斜率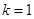 的直线
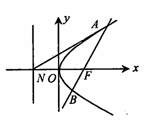
的直线 过焦点F,与抛物线交于A、B两点,若抛物线的准线与x轴交点为N,则
过焦点F,与抛物线交于A、B两点,若抛物线的准线与x轴交点为N,则 ( )
( )
 C.
C. 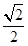 D.
D. 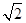
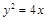 的准线过双曲线
的准线过双曲线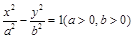 的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为
的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )