题目内容
设函数 (其中
(其中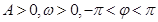 )在
)在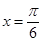 处取得最大值2,其图象与轴的相邻两个交点的距离为
处取得最大值2,其图象与轴的相邻两个交点的距离为
(I)求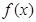 的解析式;
的解析式;
(II)求函数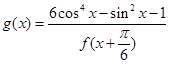 的值域。
的值域。
(1)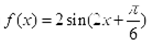 (II)
(II)
解析试题分析:(1)由题设条件可知f(x)的周期T=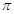 ,
,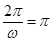 解得
解得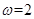
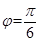
故f(x)的解析式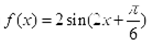
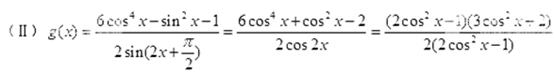
 ,因
,因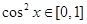 ,且
,且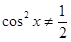 ,故
,故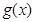 的值域为
的值域为
考点:本题考查了三角函数的化简及性质
点评:给出图象求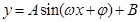 的解析式,
的解析式,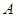 是振幅大小,一般可以观察最大值与最小值求得;
是振幅大小,一般可以观察最大值与最小值求得;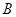 是平衡位置在y 轴上的截距;确定
是平衡位置在y 轴上的截距;确定 ,通常可由平衡点或最值点确定周期
,通常可由平衡点或最值点确定周期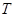 ,进而求
,进而求 。
。

练习册系列答案
相关题目
 中,
中, .
.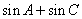 的取值范围;
的取值范围; 为锐角,求
为锐角,求 的最大值并求出此时角
的最大值并求出此时角 的大小.
的大小.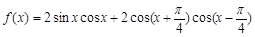 。
。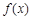 的单调递减区间; (2)设
的单调递减区间; (2)设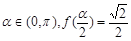 ,求
,求 的值。
的值。 (
( )的部分图像如右所示.
)的部分图像如右所示.
 的解析式;
的解析式; ,且
,且 ,求
,求 的值.
的值. 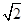 sin
sin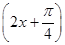 .
.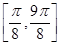 上的图象.
上的图象.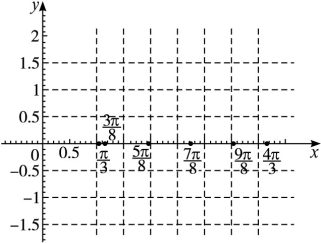
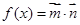 其中,
其中,
 的最小正周期及单调减区间.
的最小正周期及单调减区间.
 .
.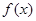 的定义域及最小正周期;
的定义域及最小正周期;
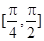 上的最值.
上的最值. , 其中
, 其中
 ,其中
,其中 若
若 相邻两对称轴间的距离不小于
相邻两对称轴间的距离不小于
 的取值范围;
的取值范围;  中,
中, 、
、 、
、 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,当
,当 求
求