题目内容
设函数f(x)=|sin(2x+ )|,则下列关于函数f(x)的说法中正确的是( )
)|,则下列关于函数f(x)的说法中正确的是( )
 )|,则下列关于函数f(x)的说法中正确的是( )
)|,则下列关于函数f(x)的说法中正确的是( )| A.f(x)是偶函数 |
| B.f(x)的最小正周期为π |
C.f(x)的图象关于点(-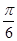 ,0)对称 ,0)对称 |
D.f(x)在区间[ , ,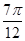 ]上是增函数 ]上是增函数 |
D
对于选项A,由于f( )=|sin(2×
)=|sin(2× +
+ )|=0,而f(-
)|=0,而f(- )=|sin[2×(-
)=|sin[2×(- )+
)+ ]|=|sin
]|=|sin |=
|= ≠f(
≠f( ),所以f(x)不是偶函数;对于选项B,由于f(x)=sin(2x+
),所以f(x)不是偶函数;对于选项B,由于f(x)=sin(2x+ )的周期为π,而f(x)=|sin(2x+
)的周期为π,而f(x)=|sin(2x+ )|的图象是将f(x)=sin(2x+
)|的图象是将f(x)=sin(2x+ )的x轴上方的图象保持不变,x轴下方的图象关于x轴对称到上方去,因此f(x)=|sin(2x+
)的x轴上方的图象保持不变,x轴下方的图象关于x轴对称到上方去,因此f(x)=|sin(2x+ )|的周期为f(x)=sin(2x+
)|的周期为f(x)=sin(2x+ )的周期的一半,故选项B不正确;对于选项C,由于f(x)=|sin(2x+
)的周期的一半,故选项B不正确;对于选项C,由于f(x)=|sin(2x+ )|的图象不是中心对称图形,因此也不正确;对于选项D,由三角函数的性质可知,f(x)=|sin(2x+
)|的图象不是中心对称图形,因此也不正确;对于选项D,由三角函数的性质可知,f(x)=|sin(2x+ )|的单调递增区间是kπ≤2x+
)|的单调递增区间是kπ≤2x+ ≤kπ+
≤kπ+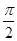 (k∈Z),即
(k∈Z),即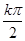 -
-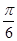 ≤x≤
≤x≤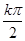 +
+ (k∈Z),当k=1时,x∈[
(k∈Z),当k=1时,x∈[ ,
,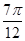 ],故选D.
],故选D.
 )=|sin(2×
)=|sin(2× +
+ )|=0,而f(-
)|=0,而f(- )=|sin[2×(-
)=|sin[2×(- )+
)+ ]|=|sin
]|=|sin |=
|= ≠f(
≠f( ),所以f(x)不是偶函数;对于选项B,由于f(x)=sin(2x+
),所以f(x)不是偶函数;对于选项B,由于f(x)=sin(2x+ )的周期为π,而f(x)=|sin(2x+
)的周期为π,而f(x)=|sin(2x+ )|的图象是将f(x)=sin(2x+
)|的图象是将f(x)=sin(2x+ )的x轴上方的图象保持不变,x轴下方的图象关于x轴对称到上方去,因此f(x)=|sin(2x+
)的x轴上方的图象保持不变,x轴下方的图象关于x轴对称到上方去,因此f(x)=|sin(2x+ )|的周期为f(x)=sin(2x+
)|的周期为f(x)=sin(2x+ )的周期的一半,故选项B不正确;对于选项C,由于f(x)=|sin(2x+
)的周期的一半,故选项B不正确;对于选项C,由于f(x)=|sin(2x+ )|的图象不是中心对称图形,因此也不正确;对于选项D,由三角函数的性质可知,f(x)=|sin(2x+
)|的图象不是中心对称图形,因此也不正确;对于选项D,由三角函数的性质可知,f(x)=|sin(2x+ )|的单调递增区间是kπ≤2x+
)|的单调递增区间是kπ≤2x+ ≤kπ+
≤kπ+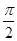 (k∈Z),即
(k∈Z),即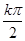 -
-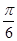 ≤x≤
≤x≤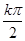 +
+ (k∈Z),当k=1时,x∈[
(k∈Z),当k=1时,x∈[ ,
,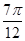 ],故选D.
],故选D.
练习册系列答案
相关题目
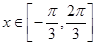
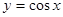 的值域;
的值域;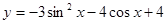 的最大值和最小值.
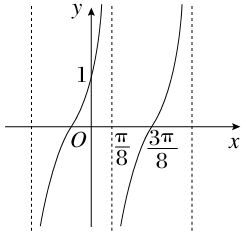
的最大值和最小值.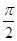 ),y=f(x)的部分图象如图所示,则f(
),y=f(x)的部分图象如图所示,则f(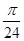 )=________.
)=________.
 ,直线x=
,直线x= 是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是( ) )
)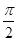 x+
x+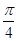 ),若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为________.
),若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为________.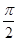 ,
,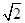 cos(
cos(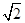 cos(-α)=-
cos(-α)=-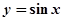 上任一点
上任一点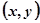 处的切线斜率为
处的切线斜率为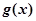 ,则函数
,则函数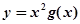 的部分图象可以是( )
的部分图象可以是( )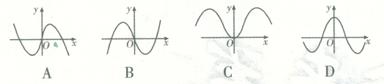
 的图象适当变化就可以得到
的图象适当变化就可以得到 的图象,这个变化可以是( )
的图象,这个变化可以是( ) 轴方向向右平移
轴方向向右平移

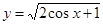 的定义域是( )
的定义域是( )


