题目内容
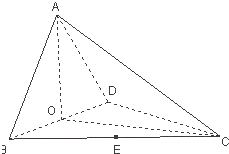 如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD=| 2 |
(I)求证:AO⊥平面BCD;
(II)求点E到平面ACD的距离;
(III)求二面角A-CD-B的余弦值.
分析:(I)如图所示,要证AO⊥平面BCD,只需证AO⊥BD,AO⊥CO即可,结合已知条件,根据勾股定理即可得到答案.
(II)以O为原点,以OB,OC,OA方向为x,y,z轴正方向,建立空间坐标系,求出平面ACD的法向量的坐标,根据点E到平面ACD的距离h=
,可求出点E到平面ACD的距离;
(III)结合(II)中结论,再由AO⊥平面BCD,即
为平面BCD的一个法向量,代入向量夹角公式,即可求出二面角A-CD-B的余弦值.
(II)以O为原点,以OB,OC,OA方向为x,y,z轴正方向,建立空间坐标系,求出平面ACD的法向量的坐标,根据点E到平面ACD的距离h=
|
| ||||
|
|
(III)结合(II)中结论,再由AO⊥平面BCD,即
| AO |
解答: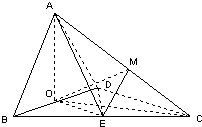 证明:(I)△ABD中,∵AB=AD=
证明:(I)△ABD中,∵AB=AD=
,O是BD中点,BD=2
∴AO⊥BD且 AO=
=1
△BCD中,连接OC∵BC=DC=2
∴CO⊥BD且 CO=
=
△AOC中AO=1,CO=
,AC=2
∴AO2+CO2=AC2故AO⊥CO
∴AO⊥平面BCD.(5分)
解:(II)如图建立空间直角坐标系,设平面ACD的法向量为
=(x,y,z)则
即
.(7分)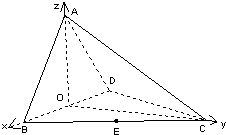
令y=1得
=(-
,1,
)是平面ACD的一个法向量..(8分)
又
=(-
,
,0)
∴点E到平面ACD的距离h=
=
.(10分)
(III)∵AO⊥平面BCD
∴
=(0,0,1)为平面BCD的一个法向量;
∴cos<
,
>=
=
则二面角A-CD-B的余弦值为
.(14分)
 证明:(I)△ABD中,∵AB=AD=
证明:(I)△ABD中,∵AB=AD=| 2 |
∴AO⊥BD且 AO=
| AB2-BO2 |
△BCD中,连接OC∵BC=DC=2
∴CO⊥BD且 CO=
| BC2-BO2 |
| 3 |
△AOC中AO=1,CO=
| 3 |
∴AO2+CO2=AC2故AO⊥CO
∴AO⊥平面BCD.(5分)
解:(II)如图建立空间直角坐标系,设平面ACD的法向量为
| n |
|
即
|

令y=1得
| n |
| 3 |
| 3 |
又
| EC |
| 1 |
| 2 |
| ||
| 2 |
∴点E到平面ACD的距离h=
|
| ||||
|
|
| ||
| 7 |
(III)∵AO⊥平面BCD
∴
| AO |
∴cos<
| AO |
| n |
| ||||
|
|
| ||
| 7 |
则二面角A-CD-B的余弦值为
| ||
| 7 |
点评:本题考查的知识点是空间直线与平面垂直的判定,空间点到平面的距离,二面角的平面角,其中(I)的关键是熟练掌握空间线线垂直与线面垂直之间的转化,(II)(III)的关键是建立空间坐标系,利用向量法解决空间距离和夹角问题.

练习册系列答案
相关题目
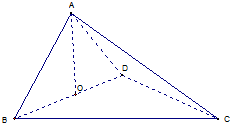 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形, 如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD=
如图,四面体ABCD中,0是BD的中点,CA=CB=CD=BD=a,AB=AD= 如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.
如图,四面体ABCD的各个面都是直角三角形,已知AB⊥BC,BC⊥CD,AB=a,BC=a,CD=c.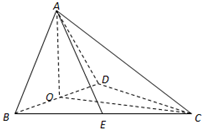 如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别是BD、BC的中点,AO⊥平面BCD,CA=CB=CD=BD=2.