题目内容
已知由实数构成的集合A满足条件:若a∈A,则 (a≠0,且a≠±1),则集合A中至少有几个元素?证明你的结论.
(a≠0,且a≠±1),则集合A中至少有几个元素?证明你的结论.
【答案】分析:由已知中若a∈A,则 (a≠0,且a≠±1),依次代入可得a、
(a≠0,且a≠±1),依次代入可得a、 、
、 和
和 均属于A,且互不相等,进而得到结论.
均属于A,且互不相等,进而得到结论.
解答:解:∵a∈A,则 ,
,
∴ ,
,
进而有 ,
,
∴又有 ,
,
∵a∈R,∴ ,
,
假设 ,则a2=-1,矛盾,
,则a2=-1,矛盾,
∴ ,
,
类似方法可证a、 、
、 和
和 四个数互不相等,
四个数互不相等,
这就证得集合A中至少有四个元素.
点评:本题考查的知识点集合元素的个数的最大值,其中根据递推式得到集合中的其它元素且证明其互不相等,是解答的核心.
 (a≠0,且a≠±1),依次代入可得a、
(a≠0,且a≠±1),依次代入可得a、 、
、 和
和 均属于A,且互不相等,进而得到结论.
均属于A,且互不相等,进而得到结论.解答:解:∵a∈A,则
 ,
,∴
 ,
,进而有
 ,
,∴又有
 ,
,∵a∈R,∴
 ,
,假设
 ,则a2=-1,矛盾,
,则a2=-1,矛盾,∴
 ,
,类似方法可证a、
 、
、 和
和 四个数互不相等,
四个数互不相等,这就证得集合A中至少有四个元素.
点评:本题考查的知识点集合元素的个数的最大值,其中根据递推式得到集合中的其它元素且证明其互不相等,是解答的核心.

练习册系列答案
相关题目
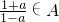 (a≠0,且a≠±1),则集合A中至少有几个元素?证明你的结论.
(a≠0,且a≠±1),则集合A中至少有几个元素?证明你的结论.