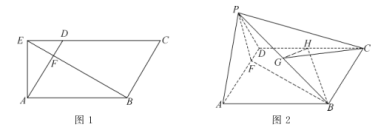
题目内容
【题目】已知椭圆方程为![]() ,其右焦点
,其右焦点![]() 与抛物线
与抛物线![]() 的焦点重合,过
的焦点重合,过![]() 且垂直于抛物线对称轴的直线与椭圆交于
且垂直于抛物线对称轴的直线与椭圆交于![]() 、
、![]() 两点,与抛物线交于
两点,与抛物线交于![]() 、
、![]() 两点.
两点.![]()
(1)求椭圆的方程;
(2)若直线l与(1)中椭圆相交于![]() ,
,![]() 两点, 直线
两点, 直线![]() ,
, ![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() (其中
(其中![]() ),且
),且![]() ,
,![]() ,
,![]() 成等比数列;设
成等比数列;设![]() 的面积为
的面积为![]() , 以
, 以![]() 、
、![]() 为直径的圆的面积分别为
为直径的圆的面积分别为![]() ,
, ![]() , 求
, 求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题意可得![]() ,
,![]() ,即得
,即得![]() ,结合
,结合![]() 可得椭圆方程;(2)设直线
可得椭圆方程;(2)设直线![]() 的方程为
的方程为![]() ,将直线方程与椭圆方程联立,写出韦达定理,由
,将直线方程与椭圆方程联立,写出韦达定理,由![]() ,
,![]() ,
,![]() 成等比数列,可解得k值,然后分别求出S,
成等比数列,可解得k值,然后分别求出S,![]() ,写出
,写出![]() 的表达式,利用基本不等式可得取值范围.
的表达式,利用基本不等式可得取值范围.
(1)由抛物线方程得![]() ,椭圆方程为
,椭圆方程为![]() ,过F垂直于抛物线对称轴的直线与椭圆交于M,N两点,可得
,过F垂直于抛物线对称轴的直线与椭圆交于M,N两点,可得![]() ,与抛物线交于C,D两点可得
,与抛物线交于C,D两点可得![]() ,
, 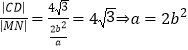 ,
, ![]() ,
,![]()
![]() ,
,
所以椭圆方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
由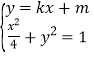 可得
可得![]() ,
,
由韦达定理: ,
,
∵![]() ,
,![]() ,
,![]() 构成等比数列,
构成等比数列,![]()
![]() ,
,
即![]()
由韦达定理代入化简得:![]() ,∵
,∵ ![]() ,
,![]()
![]() .
.
此时![]() ,即
,即![]() .
.
又由![]() 三点不共线得
三点不共线得![]() ,从而
,从而![]() .
.
故![]()
![]()
∵![]() ,
,![]() ,
,![]() ,
,
则![]()
![]() 为定值.
为定值.
![]()
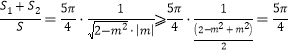 ,
,
当且仅当![]() 即
即![]() span>时等号成立.
span>时等号成立.
综上:![]() 的取值范围是
的取值范围是![]() .
.

【题目】随着互联网的兴起,越来越多的人选择网上购物.某购物平台为了吸引顾客,提升销售额,每年双十一都会进行某种商品的促销活动.该商品促销活动规则如下:①“价由客定”,即所有参与该商品促销活动的人进行网络报价,每个人并不知晓其他人的报价,也不知道参与该商品促销活动的总人数;②报价时间截止后,系统根据当年双十一该商品数量配额,按照参与该商品促销活动人员的报价从高到低分配名额;③每人限购一件,且参与人员分配到名额时必须购买.某位顾客拟参加2019双十一该商品促销活动,他为了预测该商品最低成交价,根据该购物平台的公告,统计了最近5年双十一参与该商品促销活动的人数(见下表)
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份编号t | 1 | 2 | 3 | 4 | 5 |
参与人数(百万人) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)由收集数据的散点图发现,可用线性回归模型模拟拟合参与人数![]() (百万人)与年份编号
(百万人)与年份编号![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:![]() ,并预测2019年双十一参与该商品促销活动的人数;
,并预测2019年双十一参与该商品促销活动的人数;
(2)该购物平台调研部门对2000位拟参与2019年双十一该商品促销活动人员的报价价格进行了一个抽样调查,得到如下的一份频数表:
报价区间(千元) |
|
|
|
|
|
|
频数 | 200 | 600 | 600 | 300 | 200 | 100 |
①求这2000为参与人员报价![]() 的平均值
的平均值![]() 和样本方差
和样本方差![]() (同一区间的报价可用该价格区间的中点值代替);
(同一区间的报价可用该价格区间的中点值代替);
②假设所有参与该商品促销活动人员的报价![]() 可视为服从正态分布
可视为服从正态分布![]() ,且
,且![]() 与
与![]() 可分别由①中所求的样本平均值
可分别由①中所求的样本平均值![]() 和样本方差
和样本方差![]() 估值.若预计2019年双十一该商品最终销售量为317400,请你合理预测(需说明理由)该商品的最低成交价.
估值.若预计2019年双十一该商品最终销售量为317400,请你合理预测(需说明理由)该商品的最低成交价.
参考公式即数据(i)回归方程:![]() ,其中
,其中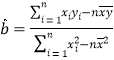 ,
,![]()
(ii)![]()
(iii)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]()
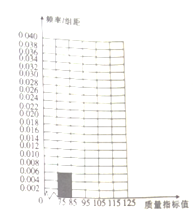
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,现用一种新配方做试验,生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
(1)将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;
(2)估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |