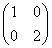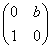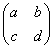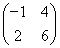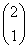Question

已知2×2矩阵M=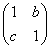,矩阵M对应的变换将点(2,1)变换成点(4,-1),求矩阵M将圆x2+y2=1变换后的曲线方程.

 

Answer 1

2x2-2xy+5y2=9

【解析】由已知得M=,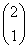

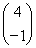即=,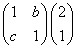

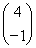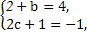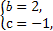∴解得∴M=.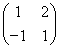

设点P(x,y)是圆x2+y2=1上的任意一点,变换后的点为P'(x',y'),则M=,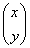

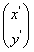所以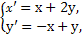从而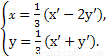

又点(x,y)在圆x2+y2=1上,

则(x'-2y')2+(x'+y')2=9,

即2x'2-2x'y'+5y'2=9,

∴圆x2+y2=1变换后的曲线方程为2x2-2xy+5y2=9.