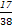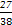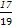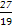题目内容
一个口袋装有n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸2个球(每次摸奖后放回),2个球颜色不同则为中奖.
(1)试用n表示一次摸奖中奖的概率.
(2)若n=5,求3次摸奖的中奖次数ξ=1的概率及数学期望.
(3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大?
(1)试用n表示一次摸奖中奖的概率.
(2)若n=5,求3次摸奖的中奖次数ξ=1的概率及数学期望.
(3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大?
(1) P=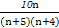 (2)
(2)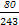
 (3) n=20
(3) n=20
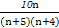 (2)
(2)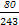
 (3) n=20
(3) n=20(1)记“1次从n+5个球中摸出2个球”为事件A,card(A)=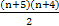 .
.
“1次从n+5个球中摸出2个球且2个球异色”为事件B,card(B)=5n,
所以,所求概率P=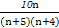 .
.
(2)3次放回式摸奖中“每次从n+5个球中摸出2个球且2个球异色”为独立重复事件,
当n=5时,获奖次数ξ~B(3, ),
),
P(ξ=1)=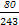 .
.
E(ξ)=np=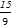 =
= .
.
(3)ξ~B(n,p),
P(ξ=1)=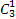 p(1-p)2=3p3-6p2+3p,0<p<1,
p(1-p)2=3p3-6p2+3p,0<p<1,
令f(p)=3p3-6p2+3p,由f'(p)=9p2-12p+3=0,
得p= ;
;
当p= 时f(p)有最大值.
时f(p)有最大值.
由p=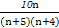 =
= ,解得n=20.
,解得n=20.
所以当n=20时,3次摸奖恰有1次中奖的概率最大.
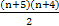 .
.“1次从n+5个球中摸出2个球且2个球异色”为事件B,card(B)=5n,
所以,所求概率P=
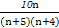 .
.(2)3次放回式摸奖中“每次从n+5个球中摸出2个球且2个球异色”为独立重复事件,
当n=5时,获奖次数ξ~B(3,
 ),
),P(ξ=1)=
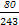 .
.E(ξ)=np=
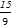 =
= .
.(3)ξ~B(n,p),
P(ξ=1)=
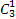 p(1-p)2=3p3-6p2+3p,0<p<1,
p(1-p)2=3p3-6p2+3p,0<p<1,令f(p)=3p3-6p2+3p,由f'(p)=9p2-12p+3=0,
得p=
 ;
;当p=
 时f(p)有最大值.
时f(p)有最大值.由p=
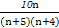 =
= ,解得n=20.
,解得n=20.所以当n=20时,3次摸奖恰有1次中奖的概率最大.

练习册系列答案
相关题目
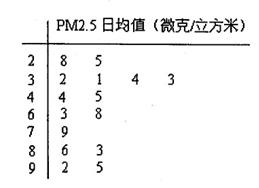
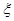 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.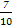 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.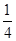
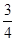
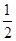
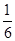
 )i,i=1,2,3,则a的值是( )
)i,i=1,2,3,则a的值是( )