题目内容
已知三点P（5，2）、F1（-6，0）、F2（6，0）
（1）求以F1、F2为焦点且过点P的双曲线的标准方程；
（2）设点P、F1、F2关于直线y=x的对称点分别为P′、
、
，求以
、
为焦点且过点P′的椭圆的标准方程．
（1）求以F1、F2为焦点且过点P的双曲线的标准方程；
（2）设点P、F1、F2关于直线y=x的对称点分别为P′、
| F | ′ 1 |
| F | ′ 2 |
| F | ′ 1 |
| F | ′ 2 |
分析：（1）利用双曲线的定义，求出a，再根据b=
，求出b，从而可得双曲线的方程；
（2）利用椭圆的定义，求出a′，再根据b′=
，求出b′，从而可得椭圆的标准方程．
| c2-a2 |
（2）利用椭圆的定义，求出a′，再根据b′=
| a2-c2 |
解答：解：（1）由题意，PF1-PF2=
-
=4
=2a，
∴a=2
，
∵c=6，∴b=
=4，
∴以F1、F2为焦点且过点P的双曲线的标准方程为
-
=1；
（2）由题意，P′（2，5）、
（0，-6）、
（0，6），
∴P′
+P′
=
+
=6
=2a′，∴a′=3
，
∵c′=6，∴b′=
=3，
∴以
、
为焦点且过点P′的椭圆的标准方程
+
=1．
| (5+6)2+22 |
| (5-6)2+22 |
| 5 |
∴a=2
| 5 |
∵c=6，∴b=
| c2-a2 |
∴以F1、F2为焦点且过点P的双曲线的标准方程为
| x2 |
| 20 |
| y2 |
| 16 |
（2）由题意，P′（2，5）、
| F | ′ 1 |
| F | ′ 2 |
∴P′
| F | ′ 1 |
| F | ′ 2 |
| 22+(5+6)2 |
| 22+(5-6)2 |
| 5 |
| 5 |
∵c′=6，∴b′=
| a2-c2 |
∴以
| F | ′ 1 |
| F | ′ 2 |
| y2 |
| 45 |
| x2 |
| 9 |
点评：本题考查双曲线、椭圆的标准方程，考查双曲线、椭圆的定义，考查学生的计算能力，正确理解双曲线、椭圆的定义是关键．
练习册系列答案
名校课堂系列答案
相关题目
（－6，0）、
（6，0）.
、
、
，求以
，求以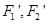
为焦点且过
点的双曲线的标准方程。