题目内容

设△A1B1C1的面积为1，点A2，B2，C2分别是边B1C1，A1C1，A1B1的中点，…，点An，Bn，Cn分别是△An-1Bn-1Cn-1的边Bn-1Cn-1，Cn-1An-1，An-1Bn-1的中点，编写一个程序，计算每个三角形的面积和这n个三角形面积的和.

解析：S=1；

sum=1；

for  i=1∶1∶n

S=S*（1/4）；

print(%io(2),S);

sum=sum+S；

end

print（% io（2），sum）；

练习册系列答案
相关题目
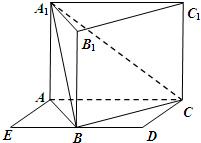精英家教网如图，侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中，AE=2，AC=AA1=4，∠E=60°，点B为DE中点．
（Ⅰ）求证：平面A1BC⊥平面A1ABB1．
（Ⅱ）设二面角A1-BC-A的大小为α，直线AC与平面A1BC所成的角为β，求sin（α+β）的值．
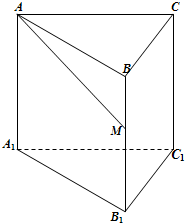精英家教网如图，已知正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞2），动点M在侧棱BB1上移动．设AM与侧面BB1C1C所成的角为θ．
（1）当θ∈[
π
6
，
π
4
]时，求点M到平面ABC的距离的取值范围；
（2）当θ=
π
6
时，求向量
AM
与
BC
夹角的大小．
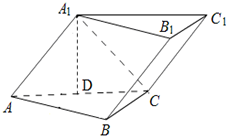如图，已知斜三棱柱（侧棱不垂直于底面）ABC-A1B1C1的侧面A1ACC1与底面ABC垂直，BC=2，AC=2
3
，AB=2
2
，AA1=A1C=
6
．
（Ⅰ） 设AC的中点为D，证明A1D⊥底面ABC；
（Ⅱ） 求异面直线A1C与AB成角的余弦值．
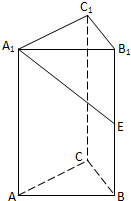（2012•嘉定区三模）如图，在正三棱柱ABC-A1B1C1中，AB=2，AA1=4．
（1）求三棱ABC-A1B1C1的表面积S；
（2）设E为棱BB1的中点，求异面直线A1E与BC所成角的大小（结果用反三角函数值表示）．
如图，斜三棱柱ABC-A1B1C1的底面是直角三角形，∠ACB=90°，点B1在底面内的射影恰好是BC的中点，且BC=CA．
（1）求证：平面ACC1A1⊥平面B1C1CB；
（2）若二面角B-AB1-C1的余弦值为-
5
7
，设
AA1
BC
=λ，求λ的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网