题目内容
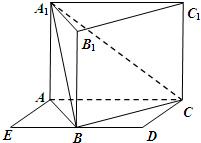 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.(Ⅰ)求证:平面A1BC⊥平面A1ABB1.
(Ⅱ)设二面角A1-BC-A的大小为α,直线AC与平面A1BC所成的角为β,求sin(α+β)的值.
分析:(1)要证明平面A1BC⊥平面A1ABB1,关键是要在一个平面内找到一条与另外一个平面垂直的直线,我可们以利用已知,证明AB⊥BC,AA1⊥BC,根据已知条件,我们有两种思路证明线线垂直的办法,进而根据线面垂直的判定定理,得到BC垂直平面A1ABB1.再由面面垂直的判定定理得到结论;
(2)由(Ⅰ)可知A1B⊥BC,AB⊥BC即∠A1BA为二面角A1-BC-A的平面角,即∠A1BA=α,由平面A1BC⊥平面A1ABB1,且平面A1BC∩平面A1ABB1=A1B,得AF⊥平面A1BC,即∠ACD为直线AC与平面A1BC所成的角,即∠ACD=β.求出α、β的三角函数值后,利用两角和的正弦公式即可得到答案,而求α、β有两种方法:一是构造三角形,解三角形;二是建立空间坐标系,利用空间向量求解.
(2)由(Ⅰ)可知A1B⊥BC,AB⊥BC即∠A1BA为二面角A1-BC-A的平面角,即∠A1BA=α,由平面A1BC⊥平面A1ABB1,且平面A1BC∩平面A1ABB1=A1B,得AF⊥平面A1BC,即∠ACD为直线AC与平面A1BC所成的角,即∠ACD=β.求出α、β的三角函数值后,利用两角和的正弦公式即可得到答案,而求α、β有两种方法:一是构造三角形,解三角形;二是建立空间坐标系,利用空间向量求解.
解答:(Ⅰ)证法一:在平行四边形ACDE中,
∵AE=2,AC=4,∠E=60°,点B为DE中点.
∴∠ABE=60°,∠CBD=30°,从而∠ABC=90°,即AB⊥BC.
又AA1⊥面ABC,BC?面ABC
∴AA1⊥BC,而AA1∩AB=A,
∴BC⊥平面A1ABB1.
∵BC?平面A1BC
∴平面A1BC⊥平面A1ABB1
证法二:∵AE=2,AC=4,∠E=60°,点B为DE中点.
∴AB=2,BC=2
,AB2+BC2=16=AC2,
∴AB⊥BC.
又AA1⊥面ABC,BC?面ABC,
∴AA1⊥BC,而AA1∩AB=A,
∴BC⊥平面A1ABB1
∵BC?平面A1BC,
∴平面A1BC⊥平面A1ABB1.
(Ⅱ)方法一:由(Ⅰ)可知A1B⊥BC,AB⊥BC
∴∠A1BA为二面角A1-BC-A的平面角,即∠A1BA=α,
在Rt△A1AB中,sinα=sin∠A1BA=
=
,cosα=
=
.
以A为原点,建立空间直角坐标系A-xyz如图所示,
其中A1(0,0,4),B(
,1,0),C(0,4,0),
=(0,4,0),
=(
,1,-4),
=(-
,3,0),
设
=(x,y,z)为平面A1BC的一个法向量,则
,∴
即
令y=1,得平面A1BC的一个法向量
=(
,1,1),则sinβ=
=
=
,
又0<β<
,∴cosβ=
=
,
∴sin(α+β)=sinαcosβ+cosαsinβ=
×
+
×
=1,
即sin(α+β)=1.(12分)
方法二:由(Ⅰ)可知A1B⊥BC,AB⊥BC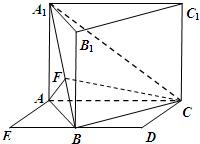
∴∠A1BA为二面角A1-BC-A的平面角,即∠A1BA=α,
在Rt△A1AB中,AB=2,AA1=4,A1B=2
,sinα=sin∠A1BA=
=
,cosα=
=
.
过点A在平面A1ABB1内作AF⊥A1B于F,连接CF,
则由平面A1BC⊥平面A1ABB1,且平面A1BC∩平面A1ABB1=A1B,得AF⊥平面A1BC
∴∠ACF为直线AC与平面A1BC所成的角,即∠ACF=β.
在Rt△ACF中,AF=
=
,sinβ=
=
,cosβ=
=
.
∴sin(α+β)=sinαcosβ+cosαsinβ=
×
+
×
=1,
即sin(α+β)=1.
∵AE=2,AC=4,∠E=60°,点B为DE中点.
∴∠ABE=60°,∠CBD=30°,从而∠ABC=90°,即AB⊥BC.

又AA1⊥面ABC,BC?面ABC
∴AA1⊥BC,而AA1∩AB=A,
∴BC⊥平面A1ABB1.
∵BC?平面A1BC
∴平面A1BC⊥平面A1ABB1
证法二:∵AE=2,AC=4,∠E=60°,点B为DE中点.
∴AB=2,BC=2
| 3 |
∴AB⊥BC.
又AA1⊥面ABC,BC?面ABC,
∴AA1⊥BC,而AA1∩AB=A,
∴BC⊥平面A1ABB1
∵BC?平面A1BC,
∴平面A1BC⊥平面A1ABB1.
(Ⅱ)方法一:由(Ⅰ)可知A1B⊥BC,AB⊥BC
∴∠A1BA为二面角A1-BC-A的平面角,即∠A1BA=α,
在Rt△A1AB中,sinα=sin∠A1BA=
| AA1 |
| A1B |
2
| ||
| 5 |
| AB |
| A1B |
| ||
| 5 |
以A为原点,建立空间直角坐标系A-xyz如图所示,
其中A1(0,0,4),B(
| 3 |
| AC |
| A1B |
| 3 |
| BC |
| 3 |
设
| n |
|
|
|
令y=1,得平面A1BC的一个法向量
| n |
| 3 |
|
| ||||
|
|
| 4 | ||
4×
|
| ||
| 5 |
又0<β<
| π |
| 2 |
| 1-sin2β |
2
| ||
| 5 |
∴sin(α+β)=sinαcosβ+cosαsinβ=
2
| ||
| 5 |
2
| ||
| 5 |
| ||
| 5 |
| ||
| 5 |
即sin(α+β)=1.(12分)
方法二:由(Ⅰ)可知A1B⊥BC,AB⊥BC

∴∠A1BA为二面角A1-BC-A的平面角,即∠A1BA=α,
在Rt△A1AB中,AB=2,AA1=4,A1B=2
| 5 |
| AA1 |
| A1B |
2
| ||
| 5 |
| AB |
| A1B |
| ||
| 5 |
过点A在平面A1ABB1内作AF⊥A1B于F,连接CF,
则由平面A1BC⊥平面A1ABB1,且平面A1BC∩平面A1ABB1=A1B,得AF⊥平面A1BC
∴∠ACF为直线AC与平面A1BC所成的角,即∠ACF=β.
在Rt△ACF中,AF=
| AA1•AB |
| A1B |
4
| ||
| 5 |
| AF |
| AC |
| ||
| 5 |
| 1-sin2β |
2
| ||
| 5 |
∴sin(α+β)=sinαcosβ+cosαsinβ=
2
| ||
| 5 |
2
| ||
| 5 |
| ||
| 5 |
| ||
| 5 |
即sin(α+β)=1.
点评:求二面角的大小,一般先作出二面角的平面角.此题是利用二面角的平面角的定义作出∠A1BA为二面角A1-BC-A的平面角,通过解∠A1BA所在的三角形求得∠A1BA.其解题过程为:作∠A1BA→证∠A1BA是二面角的平面角→计算∠A1BA,简记为“作、证、算”.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B为DE中点.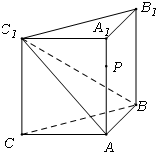 如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.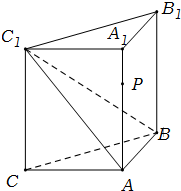 (2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•浙江模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.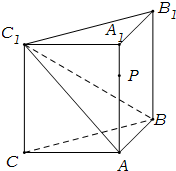 (2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
(2012•泉州模拟)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.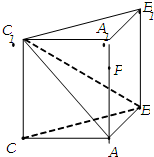 (2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).
(2013•梅州二模)如图,侧棱垂直底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0).