题目内容
数列{an}满足a1=1,an+1=2an+1(n∈N+),那么 的值为( ).
的值为( ).
 的值为( ).
的值为( ).| A.127 | B.63 | C.15 | D.31 |
B
试题分析:根据题意,由于数列{an}满足a1=1,an+1=2an+1(n∈N+) an+1+1=2(an+1),,所以{ an+1}是首项为2,公比为2的等比数列,故可知an+1=
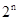 ,故可知an=
,故可知an=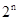 -1,故可知
-1,故可知 =63,故答案为B.
=63,故答案为B.点评:主要是考查了数列的递推关系式的运用,属于基础题。

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
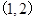 是函数
是函数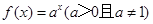 的图象上一点,数列
的图象上一点,数列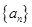 的前n项和
的前n项和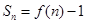 .
. 为等比数列, 其前
为等比数列, 其前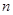 项和为
项和为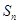 , 已知
, 已知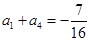 , 且对于任意的
, 且对于任意的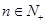 有
有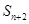 ,
, 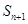 成等差;求数列
成等差;求数列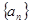 中,
中,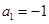 ,
,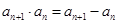 ,则数列通项
,则数列通项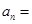 ___________
___________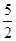 ,a1+a2+…+an=An2+Bn,n∈N+,其中A,B为常数,则AB=__________.
,a1+a2+…+an=An2+Bn,n∈N+,其中A,B为常数,则AB=__________.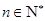 ,数列
,数列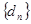 满足
满足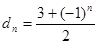 ,数列
,数列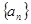 满足
满足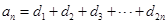 ;数列
;数列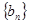 为公比大于
为公比大于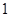 的等比数列,且
的等比数列,且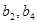 为方程
为方程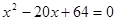 的两个不相等的实根.
的两个不相等的实根.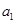 项,第
项,第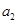 项,第
项,第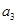 项,……,第
项,……,第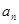 项,……删去后剩余的项按从小到大的顺序排成新数列
项,……删去后剩余的项按从小到大的顺序排成新数列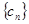 ,求数列
,求数列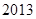 项和.
项和.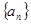 中,
中,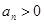 ,
,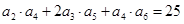 ,那么
,那么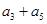 等于
等于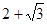 与
与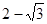 的等比中项为________________。
的等比中项为________________。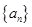 中,已知
中,已知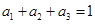 ,
,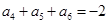 ,则该数列的前15项的和
,则该数列的前15项的和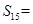 __ __.
__ __.