题目内容
已知a、b、c是△ABC的三边长,关于x的方程ax2-2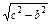 x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10
x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10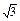 ,c=7.
,c=7.
(1)求角C;
(2)求a,b的值.
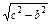 x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10
x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10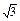 ,c=7.
,c=7.(1)求角C;
(2)求a,b的值.
(1)C=60°(2)a=8,b=5.
(1)设x1、x2为方程ax2-2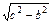 x-b=0的两根,
x-b=0的两根,
则x1+x2=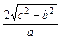 ,x1·x2=-
,x1·x2=-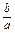 .
.
∴(x1-x2)2=(x1+x2)2-4x1x2= +
+ =4.
=4.
∴a2+b2-c2=ab.
又cosC=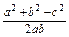 =
=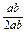 =
= ,
,
又∵C∈(0°,180°),∴C=60°.
(2)由S= absinC=10
absinC=10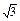 ,∴ab="40. " ①
,∴ab="40. " ①
由余弦定理c2=a2+b2-2abcosC,
即c2=(a+b)2-2ab(1+cos60°).
∴72=(a+b)2-2×40×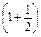 .
.
∴a+b=13.又∵a>b ②
∴由①②,得a=8,b=5.
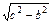 x-b=0的两根,
x-b=0的两根,则x1+x2=
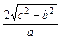 ,x1·x2=-
,x1·x2=-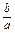 .
.∴(x1-x2)2=(x1+x2)2-4x1x2=
 +
+ =4.
=4.∴a2+b2-c2=ab.
又cosC=
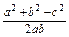 =
=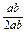 =
= ,
,又∵C∈(0°,180°),∴C=60°.
(2)由S=
 absinC=10
absinC=10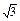 ,∴ab="40. " ①
,∴ab="40. " ①由余弦定理c2=a2+b2-2abcosC,
即c2=(a+b)2-2ab(1+cos60°).
∴72=(a+b)2-2×40×
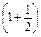 .
.∴a+b=13.又∵a>b ②
∴由①②,得a=8,b=5.

练习册系列答案
相关题目
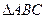 中,角
中,角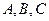 所对的边分别为
所对的边分别为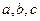 ,且
,且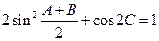 (1)求角
(1)求角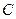 的大小
的大小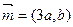 ,向量
,向量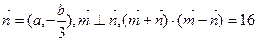 ,求
,求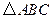 中,角
中,角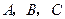 的对边分别为
的对边分别为
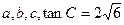 .(I)求
.(I)求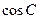 ;(II)若
;(II)若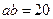 ,且
,且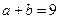 ,求
,求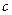 .
.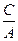 ,
,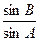 都是方程log
都是方程log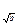 x=logb(4x-4)的根,则△ABC ( )
x=logb(4x-4)的根,则△ABC ( )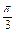 ,求角C的大小;
,求角C的大小;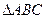 的三边长
的三边长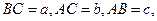
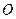 为
为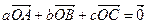 ,则点
,则点 外心
外心  内心
内心  重心
重心  垂心
垂心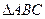 中,
中,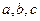 是角
是角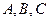 所对的边,已知
所对的边,已知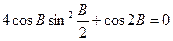 .
.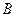 的大小;
的大小;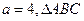 的面积为
的面积为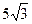 ,求
,求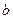 的值.
的值.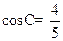 ,则角A的大小为 .
,则角A的大小为 .