题目内容
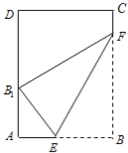
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() ,
,![]() 为椭圆
为椭圆![]() 的左焦点,椭圆的利息率为
的左焦点,椭圆的利息率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长其交抛物线
并延长其交抛物线![]() 于点
于点![]() ,
,![]() 为抛物线
为抛物线![]() 上一动点,且在
上一动点,且在![]() ,
,![]() 之间移动.
之间移动.

(1)当![]() 取最小值时,求
取最小值时,求![]() 的值;
的值;
(2)若![]() 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当![]() 的面积取最大值时,求面积最大值及此时直线
的面积取最大值时,求面积最大值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() ;
;![]()
【解析】
(1)用![]() 表示出
表示出![]() ,
,![]() ,根据基本不等式得出
,根据基本不等式得出![]() 的值,从而得出
的值,从而得出![]() 和
和![]() 的方程;
的方程;
(2)用![]() 表示出椭圆方程,联立方程组得出
表示出椭圆方程,联立方程组得出![]() 点坐标,计算出△
点坐标,计算出△![]() 的三边关于
的三边关于![]() 的式子,从而确定
的式子,从而确定![]() 的值,求出
的值,求出![]() 的距离和
的距离和![]() 到直线
到直线![]() 的距离,利用二次函数性质得出
的距离,利用二次函数性质得出![]() 面积的最大值,即可求得直线
面积的最大值,即可求得直线![]() 的方程.
的方程.
解:(1)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以当![]() 取最小值时,
取最小值时,![]() ,又因为
,又因为![]() ,所以
,所以![]() .
.
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,设椭圆的标准方程为
,设椭圆的标准方程为![]() .
.
设![]() ,
,![]() ,由
,由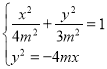 得
得![]() ,所以
,所以![]() 或
或![]() (舍去),代入抛物线方程得
(舍去),代入抛物线方程得![]() ,即
,即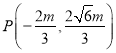 ,
,
于是![]() ,
,![]() ,
,![]() ,又因为
,又因为![]() 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以![]() .此时抛物线方程为
.此时抛物线方程为![]() ,
,![]() ,
,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .联立
.联立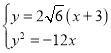 ,得
,得![]() 或
或![]() (舍去),于是
(舍去),于是![]() ,所以
,所以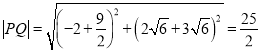 ,
,
设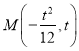 (
(![]() )到直线
)到直线![]() 的距离为
的距离为![]() ,则
,则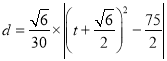 ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 的面积的最大值为
的面积的最大值为![]() .此时
.此时![]() .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |