题目内容
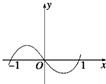9、已知y=x（x-1）（x+1）的图象如图所示，今考虑f（x）=x（x-1）（x+1）+0.01，则方程f（x）=0①有三个实根；②当x＜-1时，恰有一实根（有一实根且仅有一实根）；③当-1＜x＜0时，恰有一实根；④当0＜x＜1时，恰有一实根；⑤当x＞1时，恰有一实根．则正确结论的编号为
①②
．分析：计算f（-2）与f（-1）的值，根据根的存在性定理可知在（-2，-1）内有一个实根，结合图象可知方程f（x）=0在（-∞，-1）上，只有一个实根，故②正确，由图知f（x）=0在（-1，0）上没有实数根，所以③不正确，f（x）=0在（0，1）上有两个实根，④不正确，f（x）=0在（1，+∞）上没有实根，⑤不正确．并且由此可知①也正确．
解答：解：∵f（-2）=-2×（-3）×（-1）+0.01=-5.99＜0，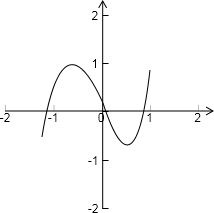
f（-1）=0.01＞0，即f（-2）•f（-1）＜0，
∴在（-2，-1）内有一个实根．
由图中知：方程f（x）=0在（-∞，-1）上，只有一个实根，
所以②正确．
又∵f（0）=0.01＞0，由图知f（x）=0在（-1，0）上没有实数根，
所以③不正确
又∵f（0.5）=0.5×（-0.5）×1.5+0.01=-0.365＜0，
f（1）=0.01＞0，即f（0.5）f（1）＜0，
所以f（x）=0．
在（0.5，1）上必有一个实根，且f（0）•f（0.5）＜0，
∴f（x）=0在（0，0.5）上也有一个实根．
∴f（x）=0在（0，1）上有两个实根，④不正确．
由f（1）＞0且f（x）在（1，+∞）上是增函数，
∴f（x）＞0，f（x）=0在（1，+∞）上没有实根．
∴⑤不正确．并且由此可知①也正确．
答案①②
f（-1）=0.01＞0，即f（-2）•f（-1）＜0，
∴在（-2，-1）内有一个实根．
由图中知：方程f（x）=0在（-∞，-1）上，只有一个实根，
所以②正确．
又∵f（0）=0.01＞0，由图知f（x）=0在（-1，0）上没有实数根，
所以③不正确
又∵f（0.5）=0.5×（-0.5）×1.5+0.01=-0.365＜0，
f（1）=0.01＞0，即f（0.5）f（1）＜0，
所以f（x）=0．
在（0.5，1）上必有一个实根，且f（0）•f（0.5）＜0，
∴f（x）=0在（0，0.5）上也有一个实根．
∴f（x）=0在（0，1）上有两个实根，④不正确．
由f（1）＞0且f（x）在（1，+∞）上是增函数，
∴f（x）＞0，f（x）=0在（1，+∞）上没有实根．
∴⑤不正确．并且由此可知①也正确．
答案①②
点评：本题主要考查了函数与方程的综合运用，以及三次函数的图象的应用，属于基础题．
练习册系列答案
相关题目
已知y=x（x-1）（x+1）的图象如图所示．令f（x）=x（x-1）（x+1）+0.01，则下列关于f（x）=0的解叙述正确的是
已知定义在R上的函数f（x）满足f（2）=1，f′（x）为f（x）的导函数．已知y=f′（x）的图象如图所示，若两个正数a，b满足f（2a+b）＞1，则
已知函数f（x）=|2|x|-2|，x∈R．