题目内容
 已知函数f(x)=|2|x|-2|,x∈R.
已知函数f(x)=|2|x|-2|,x∈R.①判断函数y=f(x)的奇偶性,并证明你的结论;
②作出函数y=f(x)的图象,并完成下列填空.
已知关于x的方程f(x)=k,则当k∈
{0}∪(1,+∞)
{0}∪(1,+∞)
时,方程有2个根;当k=1
1
时,方程有3个根;当k∈(0,1)
∈(0,1)
时,方程有4个根.分析:①由题意,本题要先判断出函数的奇偶性,再利用定义证明,直接验证f(-x)与f(x)的关系即可;
②先作出如图的图象,由图易得出方程f(x)=k的根的个数与k的取值范围的关系.
②先作出如图的图象,由图易得出方程f(x)=k的根的个数与k的取值范围的关系.
解答: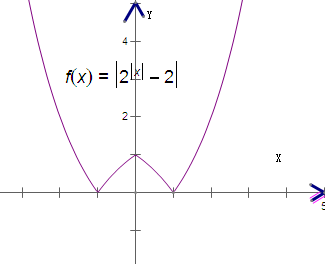 解:①函数的解析式知此函数是一个偶函数,证明如下:
解:①函数的解析式知此函数是一个偶函数,证明如下:
因为f(-x)=|2|-x|-2|=|2|x|-2|=f(x)故函数是一个偶函数;
②函数的图象如右图
由图象知,当k>1时,方程有二个根;
当k=0或1时,方程有三个根;
当0<k<1时,方程有四个根
故答案为>1; 0或1;∈(0,1)
 解:①函数的解析式知此函数是一个偶函数,证明如下:
解:①函数的解析式知此函数是一个偶函数,证明如下:因为f(-x)=|2|-x|-2|=|2|x|-2|=f(x)故函数是一个偶函数;
②函数的图象如右图
由图象知,当k>1时,方程有二个根;
当k=0或1时,方程有三个根;
当0<k<1时,方程有四个根
故答案为>1; 0或1;∈(0,1)
点评:本题研究函数奇偶性的判断,解题的关键是熟练掌握用定义法判断函数的奇偶性,本题第二小题作出准确的图象很关键,要注意把一些关键点做准确,本题考查了判断证明的能力及作图能力,是函数考查的基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|