Question

已知定义在R上的函数f（x）满足f（2）=1，f′（x）为f（x）的导函数．已知y=f′（x）的图象如图所示，若两个正数a，b满足f（2a+b）＞1，则

b-1

a-2

的取值范围是（　　）

• A．（-

  1

  2

  ，1)
• B．(-∞，-

  1

  2

  )∪(1，+∞)
• C．（-2，1）
• D．（-∞，-2）∪（1，+∞）

Answer 1

分析：先根据导函数的图象判断原函数的单调性，从而确定a、b的范围，最后利用线性规划的方法得到答案．

解答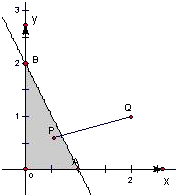：解：由图可知，当x＞0时，导函数f'（x）＜0，原函数单调递减，
∵两正数a，b满足f（2a+b）＞1，且f（2）=1，
∴2a+b＜2，a＞0，b＞0，画出可行域如图．
k=

b-1

a-2

表示点Q（2，1）与点P（x，y）连线的斜率，
当P点在A（1，0）时，k最大，最大值为：

1-0

2-1

=1；
当P点在B（0，2）时，k最小，最小值为：

1-2

2-0

=-

1

2

．
k的取值范围是（-

1

2

，1）．
故选A．

点评：本题主要考查函数的单调性与其导函数的正负之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．