题目内容
下列命题:①已知函数y=f(x)在区间[a,b]上连续,且f(a)f(b)<0,则y=f(x)在[a,b]上零点个数一定为1个;②定义在R上的奇函数f(x)必满足f(0)=0;
③f(x)=(2x+1)2-2(2x-1)既不是奇函数又不是偶函数;
④A=R,B=R,f:x→y=
| 1 |
| x+1 |
⑤f(x)=
| 1 |
| x |
其中真命题的序号是
分析:逐一检验各个选项的正确性,通过给变量取特殊值,举反例可以排除某些选项.
解答:解:①不正确,如f(x)=x(x-1)(x-2)在区[-1,3]上上连续,且f(-1)f(3)<0,f(x)在[-1,3]上的零点
有3个,零点个数为 3.
②正确,按照奇函数的定义,f(0)=f(-0)=-f(0),∴2f(0)=0,故 f(0)=0.
③不正确,∵f(x)=(2x+1)2-2(2x-1)=4x2-1,定义域为R,关于原点对称,f(-x)=f(x),
是一个偶函数.
④不正确,因为前一个集合中的-1在后一个集合中没有元素与之对应,故不是映射.
⑤不正确,因为当x=-1时 y=-1,当 x=1 时,y=1,1>-1,故 y=
在其定义域内不是减函数.
综上,只有②正确,
故答案为②.
有3个,零点个数为 3.
②正确,按照奇函数的定义,f(0)=f(-0)=-f(0),∴2f(0)=0,故 f(0)=0.
③不正确,∵f(x)=(2x+1)2-2(2x-1)=4x2-1,定义域为R,关于原点对称,f(-x)=f(x),
是一个偶函数.
④不正确,因为前一个集合中的-1在后一个集合中没有元素与之对应,故不是映射.
⑤不正确,因为当x=-1时 y=-1,当 x=1 时,y=1,1>-1,故 y=
| 1 |
| x |
综上,只有②正确,
故答案为②.
点评:本题考查函数零点的个数判断、映射的定义、函数的单调性的判断、函数的奇偶性和单调性,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.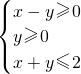 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.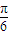 )图象的一个对称中心为点(
)图象的一个对称中心为点(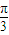 ,0);③若函数f(x)在R上满足f(x+1)=
,0);③若函数f(x)在R上满足f(x+1)=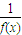 ,则f(x)是周期为2的函数;④在△ABC中,若
,则f(x)是周期为2的函数;④在△ABC中,若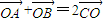 ,则S△ABC=S△BOC其中正确命题的序号为 .
,则S△ABC=S△BOC其中正确命题的序号为 .