题目内容
【题目】设函数 ![]() (x∈R),其中t∈R,将f(x)的最小值记为g(t).
(x∈R),其中t∈R,将f(x)的最小值记为g(t).
(1)求g(t)的表达式;
(2)当﹣1≤t≤1时,要使关于t的方程g(t)=kt有且仅有一个实根,求实数k的取值范围
【答案】
(1)解:由已知有: ![]() =sin2x﹣2tsinx+2t2﹣6t+1=(sinx﹣t)2+t2﹣6t+1,
=sin2x﹣2tsinx+2t2﹣6t+1=(sinx﹣t)2+t2﹣6t+1,
由于x∈R,∴﹣1≤sinx≤1,
∴当t<﹣1时,则当sinx=﹣1时,f(x)min=2t2﹣4t+2;
当﹣1≤t≤1时,则当sinx=t时,f(x)min=t2﹣6t+1;
当t>1时,则当sinx=1时,f(x)min=2t2﹣8t+2;
综上, 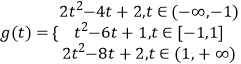
(2)解:当﹣1≤t≤1时,g(t)=t2﹣6t+1,方程g(t)=kt即t2﹣6t+1=kt,
即方程t2﹣(k+6)t+1=0在区间[﹣1,1]有且仅有一个实根,
令q(t)=t2﹣(k+6)t+1,则有:
①若△=(k+6)2﹣4=0,即k=﹣4或k=﹣8.
当k=﹣4时,方程有重根t=1;当k=﹣8时,c方程有重根t=﹣1,∴k=﹣4或k=﹣8.
② 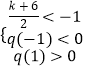
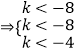 k<﹣8或
k<﹣8或 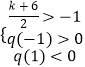
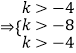 k>﹣4,
k>﹣4,
综上,当k∈(﹣∞,﹣8]∪[﹣4,+∞)时,关于t的方程g(t)=kt在区间[﹣1,1]有且仅有一个实根
【解析】(1)首先对函数f(x)进行化简整理,进而看当t<﹣1,﹣1≤t≤1和t>1时时函数f(x)的最小值,进而确定g(t)的解析式.(2)根据(1)可知当﹣1≤t≤1时函数g(t)的解析式,整理g(t)=kt得t2﹣(k+6)t+1=0问题转化为在区间[﹣1,1]有且仅有一个实根,先根据判别式等于0求得k的值,令q(t)=t2﹣(k+6)t+1,进而确定函数与x轴的轴有一个交点落在区间[﹣1,1]分别求得k的范围,最后综合可得答案.
【考点精析】根据题目的已知条件,利用函数的最值及其几何意义的相关知识可以得到问题的答案,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案