题目内容
某食品公司为了解某种新品种食品的市场需求,进行了20天的测试,人为地调控每天产品的单价P(元/件):前10天每天单价呈直线下降趋势(第10天免费赠送品尝),后10天呈直线上升,其中4天的单价记录如表:
而这20天相应的销售量Q(百件/天)与x对应的点(x,Q)在如图所示的半圆上.

(1)写出每天销售收入y(元)与时间x(天)的函数关系式y=f(x).
(2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价P定为多少元为好?(结果精确到1元)
| 时间(将第x天记为x)x | 1 | 10 | 11 | 18 |
| 单价(元/件)P | 9 | 0 | 1 | 8 |

(1)写出每天销售收入y(元)与时间x(天)的函数关系式y=f(x).
(2)在这20天中哪一天销售收入最高?为使每天销售收入最高,按此次测试结果应将单价P定为多少元为好?(结果精确到1元)
(1)y=100QP=100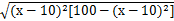 ,x∈[1,20],x∈N*
,x∈[1,20],x∈N*
(2)7
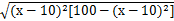 ,x∈[1,20],x∈N*
,x∈[1,20],x∈N*(2)7
(1)P=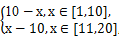 x∈N*,
x∈N*,
Q=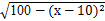 ,x∈[1,20],x∈N*,
,x∈[1,20],x∈N*,
所以y=100QP=100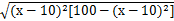 ,x∈[1,20],x∈N*.
,x∈[1,20],x∈N*.
(2)因为(x-10)2[100-(x-10)2]≤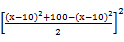 =2500,
=2500,
所以当且仅当(x-10)2=100-(x-10)2,
即x=10±5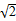 时,y有最大值.
时,y有最大值.
因为x∈N*,所以取x=3或17时,ymax=700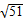
≈4999(元),此时,P=7元.
答:第3天或第17天销售收入最高,按此次测试结果应将单价P定为7元为好.
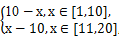 x∈N*,
x∈N*,Q=
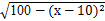 ,x∈[1,20],x∈N*,
,x∈[1,20],x∈N*,所以y=100QP=100
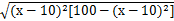 ,x∈[1,20],x∈N*.
,x∈[1,20],x∈N*.(2)因为(x-10)2[100-(x-10)2]≤
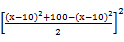 =2500,
=2500,所以当且仅当(x-10)2=100-(x-10)2,
即x=10±5
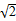 时,y有最大值.
时,y有最大值.因为x∈N*,所以取x=3或17时,ymax=700
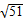
≈4999(元),此时,P=7元.
答:第3天或第17天销售收入最高,按此次测试结果应将单价P定为7元为好.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有且仅有一个解
有且仅有一个解 ,若不等式
,若不等式 成立,则实数a的取值范围是( ).
成立,则实数a的取值范围是( ). }
} }
} }
} }
}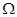 为平面直角坐标系
为平面直角坐标系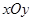 中的点集,从
中的点集,从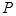 作
作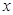 轴、
轴、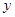 轴的垂线,垂足分别为
轴的垂线,垂足分别为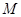 ,
,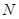 ,记点
,记点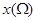 ,点
,点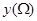 . 若
. 若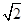 ;
;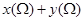 的取值范围是
的取值范围是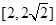 ;
;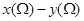 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )


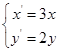
 其中0
其中0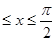
 上恒成立?
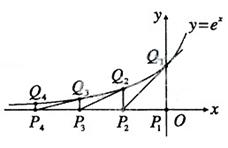
上恒成立?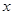 轴的垂线交曲线
轴的垂线交曲线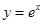 于点
于点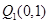 ,曲线在
,曲线在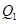 点处的切线与
点处的切线与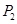 .再从
.再从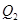 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: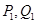 ;
;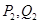 ;…;
;…;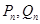 ,记
,记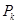 点的坐标为
点的坐标为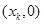 (
(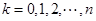 ).
).
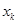 与
与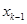 的关系(
的关系(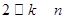 );
);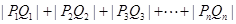 .
.