题目内容
已知数列{an}，{bn}满足a1＝1，且an、an＋1是函数f(x)＝x2－bnx＋2n的两个零点，则b10＝________．
64
【解析】依题意有anan＋1＝2n，所以an＋1an＋2＝2n＋1，两式相除得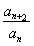
＝2，所以a1，a3，a5，…成等比数列，a2，a4，a6，…也成等比数列，而a1＝1，a2＝2，所以a10＝2×24＝32，a11＝1×25＝32，又因为an＋an＋1＝bn，所以b10＝a10＋a11＝64.
练习册系列答案
相关题目
题目内容
已知数列{an}，{bn}满足a1＝1，且an、an＋1是函数f(x)＝x2－bnx＋2n的两个零点，则b10＝________．
64
【解析】依题意有anan＋1＝2n，所以an＋1an＋2＝2n＋1，两式相除得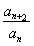＝2，所以a1，a3，a5，…成等比数列，a2，a4，a6，…也成等比数列，而a1＝1，a2＝2，所以a10＝2×24＝32，a11＝1×25＝32，又因为an＋an＋1＝bn，所以b10＝a10＋a11＝64.
