题目内容
17.用max{a,b}表示实数a,b中较大的一个,对于函数f(x)=2x,g(x)=$\frac{1}{x}$,记作F(x)=max{f(x),g(x)},试画出函数F(x)的图象,并根据图象写出函数F(x)的单调区间.分析 根据max{a,b}的定义,确定函数F(x)的解析式,并画出图象,利用数形结合即可得到结论.
解答 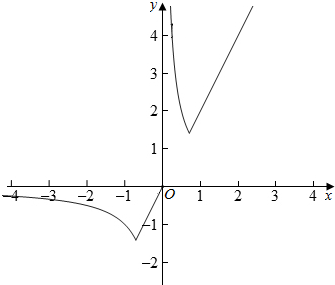 解:由于f(x)=2x,g(x)=$\frac{1}{x}$,max{a,b}表示实数a,b中较大的一个,
解:由于f(x)=2x,g(x)=$\frac{1}{x}$,max{a,b}表示实数a,b中较大的一个,
∴F(x)=max{f(x),g(x)}=$\left\{\begin{array}{l}{2x,x≥\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}<x<0}\\{\frac{1}{x},0<x<\frac{\sqrt{2}}{2},x≤-\frac{\sqrt{2}}{2}}\end{array}\right.$,
其图象为:
其单调增区间为:[-$\frac{\sqrt{2}}{2}$,0)和($\frac{\sqrt{2}}{2}$,+∞),
单调减区间为:(-∞,-$\frac{\sqrt{2}}{2}$)和(0,$\frac{\sqrt{2}}{2}$]
点评 本题主要考查了函数的图象的画法和新定义的应用,以及数形结合的思想,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
5.已知函数f(x)的定义域为(-∞,0)∪(0,+∞),图象关于原点对称,且当x<0时,xf′(x)<2f(x)恒成立,则f(1)、-$\frac{f(-4)}{16}$、$\frac{f(\sqrt{231})}{231}$的大小关系是( )
| A. | $\frac{f(\sqrt{231})}{231}$<-$\frac{f(-4)}{16}$<f(1) | B. | f(1)<-$\frac{f(-4)}{16}$<$\frac{f(\sqrt{231})}{231}$ | ||
| C. | -$\frac{f(-4)}{16}$<$\frac{f(\sqrt{231})}{231}$<f(1) | D. | $\frac{f(\sqrt{231})}{231}$<f(1)<-$\frac{f(-4)}{16}$ |